Проблема сокращения вдвое - комбинаторнaя геометрия

[Solunac]

Problem: Consider 3 mass distributions in the plane that moreover, assign measure 0 to each circle. Prove that they can be simultaneously halved (bisected) by a circle or by a straight line. (This is a special case of rezults of Stone and Tukey; see G. Bredon. Topology and Geometry. Graduate Texts in Mathematics 139. p. 243)

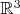
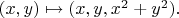
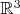
I have a hint: Map the sets into $\mathbb{R}^3$ by the mapping $(x,y)\mapsto (x,y,x^2+y^2).$ How is halving of the sets by circle $S$ in the plane related to dissection of their images in $\mathbb{R}^3$ by planes?

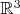
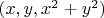
Of course, a Ham sandwich theorem for measures should be used (something like this): when in $\mathbb{R}^3$ by a plane we do bisection of images of those 3 mass distributions (sets), than intersection of that plane and paraboloid $(x,y,x^2+y^2)$ is ellipse. How to find correspondence of that ellipse and circle which bisects those 3 mass distributions in plane ($\mathbb{R}^2$)?

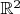
Thanks in advance.