Вы это про Виковский поворот? Мне кажется, что лучше рассмотреть конкретный пример. Вот при интегрировании по

интеграл формально расходится покольку при

подинтегральная функция осциллирует
![$$
\int \mathscr{D}\phi(x) e^{i\int dt dx \left[\frac{1}{2}(\partial \phi)^2- \frac{1}{2}m^2 \phi^2\right]}
$$ $$
\int \mathscr{D}\phi(x) e^{i\int dt dx \left[\frac{1}{2}(\partial \phi)^2- \frac{1}{2}m^2 \phi^2\right]}
$$](https://dxdy-03.korotkov.co.uk/f/2/1/8/218f66830ae92969d9177a3562776a8582.png)
проблему можно решить заменой

,
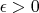
. Похожая ситуация, насколько я понимаю, возникает, например, при вычислении функции Грина, которое сводится к вычислению интеграла типа

В точке

подинтегральная функция расходится. Здесь можно опять провернуть тот же прием. Аналогично, можно все реализовать в рамках обобщенных функций, которые полностью корректны с математической точки зрения. Ну Вы это сами знаете...
А фокус Вика в том, что переход к комплексному времени мат. эквивалентен замене

.