Скалярное поле

осциллирует в кубическом резонаторе со стороной L (0 <= x,y,z <= L, координаты декартовы). На стенках резонатора поле равно 0.
Функционал действия поля имеет вид

а) найти наименьшую частоту собственных колебаний, которая соответствует трехкратному вырождению при U≡0;
б) как расщепитя эта частота, если

где

- вектора,

константа
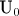
имеет порядок и размерность величины

Если найдете ответ (хотя бы к пунку а) и подскажите, как решать, я буду очень благодарен.