1) Какая точка перейдет в бесконечность?
2) Какая точка симметрична точке из п. 1. относительно окружности

?
3) Куда перейдет точка из п.2. ?
Ну а можно еще проще, учитывая, что у Вас все симметрично относительно действительной оси. Посмотрите куда перейдет точки
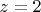
и

, и возьмите середину.