Для любого целого

сумма

где

и

- натуральные числа, не равна

где

натуральное число.
Положим, без ограничения общности дальнейших рассуждений, что

где

- натуральное число. Тогда сумма

запишется в виде
![$ (u + y)^{n} + y^{n} = u^{n} + nu^{n -
1}y + [n(n - 1)/2]u^{n - 2}y^{2} + \ldots + nuy^{n - 1} + 2y^{n} =
y^{n}( u^{n}/y^{n} + nu^{n - 1}/y^{n - 1} + [n(n - 1)/2]u^{n -
2}/y^{n - 2} + \ldots + nu/y + 2). $ $ (u + y)^{n} + y^{n} = u^{n} + nu^{n -
1}y + [n(n - 1)/2]u^{n - 2}y^{2} + \ldots + nuy^{n - 1} + 2y^{n} =
y^{n}( u^{n}/y^{n} + nu^{n - 1}/y^{n - 1} + [n(n - 1)/2]u^{n -
2}/y^{n - 2} + \ldots + nu/y + 2). $](https://dxdy-01.korotkov.co.uk/f/c/a/7/ca70b9724a76d70a2da38591ae6d7cea82.png)
Обозначим

Тогда
![$$ x^{n} + y^{n} = (u + y)^{n} + y^{n} = y^{n}(w^{n} + nw^{n - 1} +
[n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) \ne z^{n} .$$ $$ x^{n} + y^{n} = (u + y)^{n} + y^{n} = y^{n}(w^{n} + nw^{n - 1} +
[n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) \ne z^{n} .$$](https://dxdy-02.korotkov.co.uk/f/5/a/e/5ae9fc36e9fd2956574a5f9a3a199c2382.png)
Это утверждение доказывается от противного. Предположим, что многочлен
![$ y^{n}F(w) = y^{n}(w^{n}
+ nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) = z^{n} $ $ y^{n}F(w) = y^{n}(w^{n}
+ nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2) = z^{n} $](https://dxdy-04.korotkov.co.uk/f/3/f/8/3f85185ab7e52043f4286e3adeae4fea82.png)
![$ F(w)
= w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 = z^{n}/y^{n} =
\alpha^{n} $ $ F(w)
= w^{n} + nw^{n - 1} + [n(n - 1)/2]w^{n - 2} + \ldots + nw + 2 = z^{n}/y^{n} =
\alpha^{n} $](https://dxdy-01.korotkov.co.uk/f/8/a/2/8a21a772ac62dc9dcf77bff797209ca382.png)
где

рациональное положительное число.

для

. Необходимо найти
рациональное

, при котором
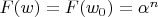
. Согласно теоремы Бюдана-Фурье и следствия из него правила
(теоремы) Декарта многочлен
![$ F_{\alpha}(w) = w^{n} + nw^{n - 1} + [n(n -
1)/2]w^{n - 2} + \ldots + nw + 2 - \alpha^{n} $ $ F_{\alpha}(w) = w^{n} + nw^{n - 1} + [n(n -
1)/2]w^{n - 2} + \ldots + nw + 2 - \alpha^{n} $](https://dxdy-02.korotkov.co.uk/f/9/2/d/92d402bf7c76b14dbfec1d72003eca5282.png)
имеет только один и притом
строго положительный корень, так как

имеет всего лишь
одну перемену знаков в системе своих коэффициентов [1]. Свободный член
![$ 2 -
\alpha^{n} < 0, \alpha > \sqrt[n]{2} > 1 $ $ 2 -
\alpha^{n} < 0, \alpha > \sqrt[n]{2} > 1 $](https://dxdy-02.korotkov.co.uk/f/9/f/5/9f58ffc643cde40ecbd03738e879db2a82.png)
. Подставив, в

значение

, получим
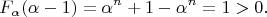
Затем, подставив, в

значение
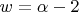
получим
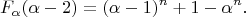
Так как
![$ \alpha > \sqrt[n]{2} > 1 $ $ \alpha > \sqrt[n]{2} > 1 $](https://dxdy-03.korotkov.co.uk/f/e/9/b/e9b8f816fe35aa7f696d85ae4885c3fe82.png)
, то можно записать

, где
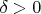
. Тогда
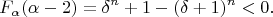
Значит единственный положительный корень

многочлена

,

не является
целым числом и равен
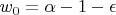
, где
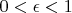
и

- рационально. Подставив

в
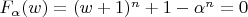
, получим

. Представив

в
виде

, где рациональная величина
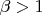
, и подставив в уравнение
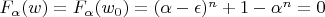
, получим уравнение

. Собственно говоря,
уравнение для бесконечного спуска получено. Можно переписать это уравнение в виде
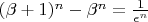
, т.е. замена (сдвиг)

на

или в более симметричном виде

т.е. замена (сдвиг)

на
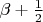
.
Рассмотрим уравнение (*) при

.

После раскрытия скобок и приведения подобных членов получаем

Далее
запишем рациональную величину

в виде
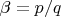
, где

- натуральные,
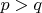
и
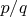
есть несократимая дробь. Тогда уравнение (***) запишется в следующем виде
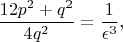
откуда
![$$ \sqrt[3]{\frac{12p^{2} + q^{2}}{4q^{2}}} = \frac{1}{\epsilon} $$ $$ \sqrt[3]{\frac{12p^{2} + q^{2}}{4q^{2}}} = \frac{1}{\epsilon} $$](https://dxdy-01.korotkov.co.uk/f/4/7/0/47046003e9f430826a4fcad60438939f82.png)
Подкоренное выражение необходимо рассмотреть для трех пар значений

:
1)

четное,
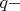
нечетное;
2)

нечетное,
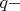
нечетное;
3)

нечетное,
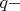
четное.
В случаях 1 и 2
![$$ \sqrt[3]{\frac{12p^{2} + q^{2}}{4q^{2}}} = \frac{1}{2q}\sqrt[3]{2q(12p^{2} + q^{2})} $$ $$ \sqrt[3]{\frac{12p^{2} + q^{2}}{4q^{2}}} = \frac{1}{2q}\sqrt[3]{2q(12p^{2} + q^{2})} $$](https://dxdy-04.korotkov.co.uk/f/f/5/d/f5da3641f6e40b342b6896a228ff92cd82.png)
Под корнем третьей степени стоит четное число из трех множителей, два из которых
нечетны, так как
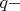
нечетное, и один равен 2. Очевидно, что
кубический корень из этого числа есть число иррациональное. В случае 3
![$$
\sqrt[3]{\frac{12p^{2} + q^{2}}{4q^{2}}} = \sqrt[3]{\frac{4(3p^{2} +
q_{1}^{2})}{4q^{2}}},
$$ $$
\sqrt[3]{\frac{12p^{2} + q^{2}}{4q^{2}}} = \sqrt[3]{\frac{4(3p^{2} +
q_{1}^{2})}{4q^{2}}},
$$](https://dxdy-04.korotkov.co.uk/f/b/2/9/b29537b70ec52e5b2cc5a8df6de44fb182.png)
где
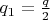
может быть как числом четным так и нечетным.
Множитель в числителе подкоренного выражения
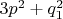
не
является кубом целого числа. Нетрудно видеть, что разность
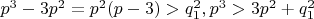
для всех значений
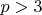
, так как
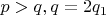
. Для

проверяется непосредственно равно ли кубу целого числа выражение
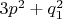
. Для

и для
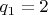
получается соответственно
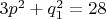
и
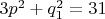
. Очевидно, что числа 28 и 31 не являются кубами целых
чисел.
Далее, случай 3 необходимо рассмотреть в трех вариантах:
3.1. Число

в своем каноническом разложении на простые множители
имеет один множитель 2, т.е.
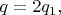
где
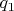
- нечетно.
![$$ \sqrt[3]{\frac{12p^{2} +
q^{2}}{4q^{2}}} = \frac{1}{2q}\sqrt[3]{2q(12p^{2} + q^{2})} $$ $$ \sqrt[3]{\frac{12p^{2} +
q^{2}}{4q^{2}}} = \frac{1}{2q}\sqrt[3]{2q(12p^{2} + q^{2})} $$](https://dxdy-02.korotkov.co.uk/f/d/7/0/d7018680deedebd52754fbbb3ecf680f82.png)
В этом случае,
чтобы из подкоренного выражения
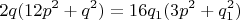
извлекался кубический корень, необходимо положить, что
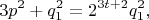
где
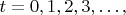
т.е.
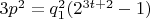
, откуда
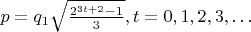
.
При
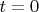
получается

, что не имеет смысла,
так как
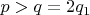
. Далее, нетрудно показать для всех

числитель
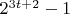
не является квадратом нечетного числа
и значит

- иррационально
(в самом деле
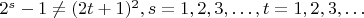
. Пусть
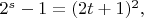
откуда
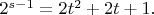
При

получается
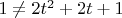
, а для всех
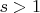
- число
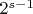
-
четное, а число

нечетное, т.е.
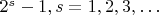
не является квадратом нечетного числа).
3.2. Число

в своем каноническом разложении на простые множители
имеет количество множителей 2 кратное 3, т.е.

нечетно. Тогда
![$$ \sqrt[3]{2q(12p^{2} + q^{2})} =
\sqrt[3]{8*2^{3t}q_1(3p^{2} + 2^{6t - 2}q_1^{2})} = 2^{(t + 1)} \sqrt[3]{q_1(3p^{2} +
2^{6t - 2}q_1^{2})} $$ $$ \sqrt[3]{2q(12p^{2} + q^{2})} =
\sqrt[3]{8*2^{3t}q_1(3p^{2} + 2^{6t - 2}q_1^{2})} = 2^{(t + 1)} \sqrt[3]{q_1(3p^{2} +
2^{6t - 2}q_1^{2})} $$](https://dxdy-03.korotkov.co.uk/f/2/0/0/200ef60fba4544cb5233763f0f84eb7e82.png)
Подкоренное выражение должно быть кубом нечетного числа,
откуда следует, что
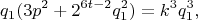
где рациональное
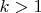
. Для

получаем равенство
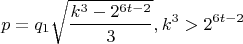
Подкоренное выражение не является квадратом целого числа

и значит

- иррационально.
3.3. Число

в своем каноническом разложении на простые множители
имеет количество множителей 2 большее единицы, но не кратное 3, т.е.
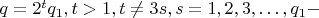
нечетно. Тогда в подкоренном выражении
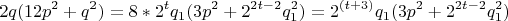
множители
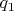
и
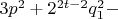
нечетны, а из четного
множителя
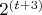
кубический корень не извлекается. Из равенства
![$ \sqrt[3]{\frac{12p^{2} + q^{2}}{4q^{2}}} = \frac{1}{\epsilon} $ $ \sqrt[3]{\frac{12p^{2} + q^{2}}{4q^{2}}} = \frac{1}{\epsilon} $](https://dxdy-02.korotkov.co.uk/f/d/3/5/d35f3fe50aa45d3805b5599c1412199982.png)
следует, что
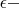
иррациональное число.
Из всех вышерассмотренных случаев вытекает, что в уравнении (***)

является иррациональным числом. Следовательно последняя низшая ступень
бесконечного спуска уравнения (*), начиная с любого значения

,
приводит к выводу, что для любого целого

сумма
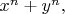
где

и

- натуральные числа, не
равна

где

натуральное число.
Наконец сам спуск практически нетрудно построить следующим образом. Уравнение (*)
переписывается в виде
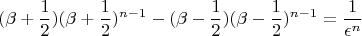
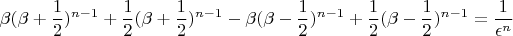
![$$ \beta[(\beta + \frac{1}{2})^{n - 1} - (\beta
- \frac{1}{2})^{n - 1}]+ \frac{1}{2}[(\beta + \frac{1}{2})^{n - 1} + (\beta -
\frac{1}{2})^{n - 1}] = \frac{1}{\epsilon^{n}} $$ $$ \beta[(\beta + \frac{1}{2})^{n - 1} - (\beta
- \frac{1}{2})^{n - 1}]+ \frac{1}{2}[(\beta + \frac{1}{2})^{n - 1} + (\beta -
\frac{1}{2})^{n - 1}] = \frac{1}{\epsilon^{n}} $$](https://dxdy-01.korotkov.co.uk/f/0/2/a/02af3e3a7aee8af6d15c6d305072547482.png)
![$$ (\beta +
\frac{1}{2})^{n - 1} - (\beta - \frac{1}{2})^{n - 1} = \frac{1}{\beta \epsilon^{n}} -
\frac{1}{2\beta}[(\beta + \frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] $$ $$ (\beta +
\frac{1}{2})^{n - 1} - (\beta - \frac{1}{2})^{n - 1} = \frac{1}{\beta \epsilon^{n}} -
\frac{1}{2\beta}[(\beta + \frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] $$](https://dxdy-04.korotkov.co.uk/f/7/e/3/7e3c043c3e15aaf79482dee66bc6015382.png)
Обозначая
![$$ \frac{1}{\beta \epsilon^{n}} - \frac{1}{2\beta}[(\beta +
\frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] = \frac{1}{\epsilon^{n - 1}} $$ $$ \frac{1}{\beta \epsilon^{n}} - \frac{1}{2\beta}[(\beta +
\frac{1}{2})^{n - 1} + (\beta - \frac{1}{2})^{n - 1}] = \frac{1}{\epsilon^{n - 1}} $$](https://dxdy-01.korotkov.co.uk/f/8/2/3/8233a947e984c9ffe85e936b916cd3be82.png)
получим
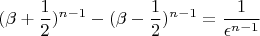
Далее, продолжая аналогичным образом, спускаясь
по лестнице, приходим к уравнению (***).
I. Рассмотрим однородное диофантово уравнение вида

при этом

- целые ,

Постановка задачи - принадлежат ли решения этого уравнения кольцу целых чисел

при различных значениях показателя

[2],[3],[4],[5],[6].
Нетрудно видеть, что уравнение (1) при

имеет целочисленные решения. Например, при
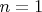
значения

и

а при
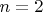
значения

и

удовлетворяют уравнению (1).
Далее утверждается, что уравнение (1) при

не имеет натуральных
решений

, т.е.

.
Доказательство этой старой задачи строится от противного, что и было изложено выше.
Расширение задачи.
II. Далее, если рассматривать (1) для всех целых

, то равенство в (1) возможно только для

. Легко видеть, при

(получается 2 = 1) равенство не выполняется.
Рассмотрим (1) с показателем степени

.

- не равные нулю целые числа.
Нетрудно видеть, что для

равенство имеет место, например, при четных равных друг другу

и

- целое.
При

и, к примеру, при

и

равенство (1) выполняется.
Пусть

, тогда (1) запишется так:

где

.
Ясно, что в (2)

и

.

Пусть

целое, тогда правая часть (3) есть

- ая степень целого числа. Из доказанного выше в разделе I следует, что (3) не имеет целочисленных решений для всех значений показателя степени

и, следовательно, равенство (1) не выполняется для всех

, если

- не равные нулю, целые числа.
III. Пусть в (1) для всех целых

, числа

- рациональные, т.е.

, где

- целые,
не равные нулю, числа.
IV. Пусть в (1) для всех целых

, числа

- иррациональные.
V. Пусть в (1) для
всех целых

, числа

-
комплексные, т.е.

,
где

, а числа

-
вещественные.
Для задач III, IV, V определить условия равенства.
Литература.
1. Курош А. Г. Курс высшей алгебры. М.: Наука, изд. 9-е, 1968.
2. Эдвардс Г. М. Последняя теорема Ферма. Генетическое введение в
алгебраическую теорию чисел. -М.: МИР, 1980.
3. Куликов Л. Я. Алгебра и теория чисел. -М.: Высшая школа,
1979.
4. Блинов В. Ф. Великая теорема Ферма: Исследование проблемы -М.: Изд-во
ЛКИ,2008.
5. Постников М. М. Теорема Ферма. Введение в теорию алгебраических
чисел. -М.: Наука, 1978.
6. Рибенбойм П. Последняя теорема Ферма для любителей. -М : Мир, 2003.