Непрерывные функции на действительных числах

[Профессор Снэйп]

Пусть $f_y(x) = f(y,x)$ --- функция из $\mathbb{R}^2$ в $\mathbb{R}$, такая что $\{ f_y : y \in \mathbb{R} \}$ есть множество всех непрерывных функций из $\mathbb{R}$ в $\mathbb{R}$. Показать, что

1) Функция $f$ не является непрерывной функцией из $\mathbb{R}^2$ в $\mathbb{R}$;
2) Множество точек разрыва функции $f$ является множеством второй категории.

Нашёл эту задачу, разбирая старые студенческие тетради. Там только условие. Первый пункт вроде очевиден, а второй что-то не получается

[id]

Профессор Снэйп
А с какой стороны Вы посмотрели на первый пункт, что решение стало очевидным?
Мне пришла, увы, только такая дефективная идея:

От противного.
Рассмотрим $C(\mathbb R)$ как счетнонормированное пространство, которое к тому же будет пространством Фреше.
Тогда отображение $I: \mathbb R \to C(\mathbb R), \ I(y) = f(\cdot,y)$ будет непрерывным.
При этом $C(\mathbb R) = \bigcup\limits_{n=1}^{\infty} I([-n,n])$.
При этом каждое $I([-n,n])$ компактно. Мне кажется, что оно к тому же еще и не имеет внутренних точек, и значит нигде не плотно (надо рассмотреть стандартный шарик в полинормированной топологии относительно какой-то из суп-норм).
Тогда получаем противоречие с теоремой Бэра, ибо $C(\mathbb R)$ полно и не есть счетное объединение нигде не плотных.

[Профессор Снэйп]

id в сообщении #318981 писал(а):

с какой стороны Вы посмотрели на первый пункт, что решение стало очевидным?

Если $f$ непрерывна как функция из $\mathbb{R}^2$ в $\mathbb{R}$, то $g(x) = f(x,x)+1$ --- непрерывная функция из $\mathbb{R}$ в $\mathbb{R}$ и для некоторого $y_0 \in \mathbb{R}$ имеем $g(x) = f_{y_0}(x)$ при всех $x \in \mathbb{R}$. Но тогда $f(y_0,y_0) = f_{y_0}(y_0) = g(y_0) = f(y_0,y_0)+1$; противоречие.

[Ales]

Профессор Снэйп в сообщении #318994 писал(а):

id в сообщении #318981 писал(а):

с какой стороны Вы посмотрели на первый пункт, что решение стало очевидным?

Если $f$ непрерывна как функция из $\mathbb{R}^2$ в $\mathbb{R}$, то $g(x) = f(x,x)+1$ --- непрерывная функция из $\mathbb{R}$ в $\mathbb{R}$ и для некоторого $y_0 \in \mathbb{R}$ имеем $g(x) = f_{y_0}(x)$ при всех $x \in \mathbb{R}$. Но тогда $f(y_0,y_0) = f_{y_0}(y_0) = g(y_0) = f(y_0,y_0)+1$; противоречие.

Красиво.

[Профессор Снэйп]

Насчёт красоты не спорю, но для тех, кто занимается теорией вычислимости подобная "диагональ" --- первое, что приходит в голову.

[Профессор Снэйп]

Взглянем на ситуацию со стороны общего понятия универсальной функции. Где-то я его уже вводил, но лучше ввести ещё раз. Вреда не будет.

Пусть $\mathcal{F}$ --- класс функций из $Y$ в $Z$. Пусть $f$ --- функция из $X \times Y$ в $Z$. Для $x \in X$ и $y \in Y$ вместо $f(x,y)$ будем также писать $f_x(y)$. Чаще всего эту запись будем использовать для случая, когда аргумент $x \in X$ фиксирован, $y$ меняется, "пробегая" множество $Y$ и функция рассматривается как функция из $Y$ в $Z$. В частности, для каждого $x \in X$ корректна запись $f_x : Y \to Z$.

Скажем, что функция $f$ является универсальной функцией для класса $\mathcal{F}$, если $\mathcal{F} = \{ f_x : x \in X \}$.

Ясно, что для каждого множества $\mathcal{F}$ функций из $Y$ в $Z$ существует универсальная функция $f : X \times Y \to Z$ в случае, если $|\mathcal{F}| \leqslant |X|$. Поскольку непрерывных функций из $Y = \mathbb{R}$ в $Z = \mathbb{R}$ всего континуум, то существует универсальная функция для класса всех одноместных непрерывных функций с $X = \mathbb{R}$.

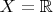
Вопросы о существовании универсальной функции с различными дополнительными свойствами более интересен. Так, например, выше было доказано, что не существует универсальной непрерывной функции для класса всех одноместных непрерывных функций. Могу накинуть ещё несколько похожих задач:

a) Доказать, что не существует универсальной функции-многочлена от двух переменных (то есть функции из $\mathbb{R}[x,y]$) для класса $\mathbb{R}[x]$ всех функций-многочленов от одной переменной.

b) Доказать, что существует универсальная непрерывная функция для класса $\mathbb{R}[x]$ всех функций-многочленов от одной переменной.

c) Выяснить, существует ли универсальная непрерывная функция $f : X \times \mathbb{R} \to \mathbb{R}$ для класса всех непрерывных функций из $\mathbb{R}$ в $\mathbb{R}$ от одной переменной, у которой $X \neq \mathbb{R}$ (то есть $X$ не обязательно континуально, а если даже континуально, то топология на $X$ не гомеоморфна стандартной топологии на действительной прямой).

-- Пт май 14, 2010 00:51:08 --

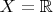
P. S. Н-да, пункт (c), конечно же, можно решить, введя на $X = \mathbb{R}$ дискретную топологию. Так что лучше спросить, какую слабейшую топологию на $\mathbb{R}$ нужно задать для того, чтобы существовала универсальная непрерывная функция.

Пункт (a) ваще очевиден; там, помимо диагонали, можно рассматривать степени многочленов.

А вот пункт (b) интересен