В какой-то из прошлых тем уже вопрошал про теорему Дьедонне-Шварца, в этой будут кое-какие доп. вопросы.
Обозначения: сопряженное пространство к

- через

;
сопряженный оператор к непр. линейному оператору

(т.е. действующий на элемент


) обозначается через

. Известно, что если

- ЛВП, то

будет действовать из

в

и будет непрерывным в сильной и *-слабой топологиях.
Цитата:
Теорема:
Пусть
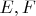
- пространства Фреше, т.е. полные метризуемые ЛВП. Пусть

- непрерывный линейный оператор. Тогда равносильны
1)

замкнуто в

2)

*-слабо замкнуто в

Замечание: известно, что если

- ЛВП, то в нем замыкание и слабое замыкание любого выпуклого множества совпадают. В частности это так для подпространств.
Проблема в том, что мне дано, что

замкнуто в сильной топологии

(т.е. в топологии сходимости на ограниченных множества из

), а нужно свести ко второму пункту теоремы. Да, если бы была не *-слабая, а просто слабая замкнутость, то я бы воспользовался замечанием выше. Но...
Таким образом, возникает два вопроса
1) Следует ли *-слабая замкнутость из сильной замкнутости и замечания выше.
2) А что будет, если исходной пр-во

монтелевское? Ведь тогда оно вроде как рефлексивно (в смысле Бурбаки, Топологические векторные пространства), а (по крайней мере для нормированных пространств известно что) в этом случае слабая и *-слабая топологии на

совпадают.
-- Сб май 08, 2010 14:04:59 --И еще. А не хватило бы для совпадения слабой и *-слабой топологии в сопряженном пространстве
 полурефлексивности
полурефлексивности исходного

, т.е. когда

алгебраически совпадает с

, где

наделяется сильной топологией?