Свойство борелевских функций

[Бабай]

Привет!

Не могли бы Вы пожалуйста проверить ниже следующее доказательство, что:

Любая неотрицательная борелевская функция является поточечным пределом неубывающей последовательности неотрицательных ступенчатых функций.

Может это и стандартый результат, но я нигде не искал его док-во, а попытался сам его обосновать. Хотелось бы знать, насколько хорошо мне это удалось сделать. Заранее большое спасибо.

Это значит, что если $f:\bb{R}^n\rightarrow[0,+\infty)$ -- борелевская функция, то существует такая последовательность неотрицательных ступенчатых функций $(f_n)_{n\in\bb{N}}$, что:

1. $\forall{}n\in\bb{N}: f_n\le{}f_{n+1}$;
2. $\forall\mbf{x}\in\bb{R}^n: f(\mbf{x})=\lim_{n\to\infty}f_n(\mbf{x})$


ДОК-ВО: Определим элементы искомой последовательности $(f_n)_{n\in\bb{N}}$ следующим образом:

$\displaystyle f_n(\mbf{x}):=\sum_{i=1}^{n2^n}\frac{i-1}{2^n}\mbf{I}_{[\frac{i-1}{2^n},\frac{i}{2^n})}(f(\mbf{x}))+n\mbf{I}_{[n,+\infty)}(f(\mbf{x}))$
или


$\displaystyle f_n(\mbf{x}):=\sum_{i=1}^{n2^n}\frac{i-1}{2^n}\mbf{I}_{\{\mbf{x}:\frac{i-1}{2^n}\le f(\mbf{x})<\frac{i}{2^n}\}}(\mbf{x})+n\mbf{I}_{\{\mbf{x}:f(\mbf{x})\ge n\}}(\mbf{x})$



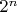
1. Очевидно, что полуинтервал $[0,+\infty)$ разбивается на полуинтервалы $[0,n)$ и $[n,+\infty)$. В свою очередь полуинтервал $[0,n)$ разбивается на $n2^n$ частей, а именно он содержит $n$ полуинтервалов $[k,k+1)$, где $k=0,...,n-1$, каждый из которых разбит на $2^n$ интервалов $[k+\frac{j}{2^n},k+\frac{j+1}{2^n})$, где $j=0,...,2^n-1$. Значение $f(\mbf{x})$ может попасть в любой из этих в общей сложности $n2^n+1$ интервалов.

Пусть $\mbf{x}$ таково, что $f(\mbf{x})\in[n,+\infty)$. Тогда $f_n(\mbf{x})=n$. При вычислении $f_{n+1}(\mbf{x})$ полуинтервал $[n,+\infty)$ разбивается на $2^{n+1}+1$ интервалов, а именно $[n+1,+\infty)$ и $2^{n+1}$ подинтервалов вида $[n+\frac{j}{2^{n+1}},n+\frac{j+1}{2^{n+1}})$, где $j=0,...,2^{n+1}-1$. Теперь видно, что $f_{n+1}(\mbf{x})=n+\frac{l}{2^{n+1}}$, где $l=0,...,2^{n+1}$ принимает свои значения в зависимости от расположения $f(\mbf{x})$. Но в любом случае $f_n(\mbf{x}) \le f_{n+1}(\mbf{x})$.

Пусть теперь $\mbf{x}$ таково, что $f(\mbf{x})\in[k+\frac{j_1}{2^n},k+\frac{j_1+1}{2^n})$ для каких-либо $k=0,...,n-1$ и $j_1=0,...,2^n-1$. Тогда $f_n(\mbf{x})=\frac{i_1-1}{2^n}$, где $i_1=2^nk+j_1+1$. Вычисляя теперь $f_{n+1}(\mbf{x})$, замечаем, что каждый полуинтервал $[k+\frac{j_1}{2^n},k+\frac{j_1+1}{2^n})$ для каждого $k$ и $j_1$ делится на две части, то есть теперь $f(\mbf{x})$ может лежать либо в $[k+\frac{j_1}{2^{n}},k+\frac{j_1}{2^{n}}+\frac{1}{2^{n+1}})$ либо в $[k+\frac{j_1}{2^{n}}+\frac{1}{2^{n+1}},k+\frac{j_1+1}{2^{n}})$. Соответственно получаем $f_{n+1}(\mbf{x})=\frac{i_2-1}{2^{n+1}}$, где либо $i_2=2^{n+1}k+2j_1+1$ либо $i_2=2^{n+1}k+(2j_1+1)+1$. Таким образом, можно ввести новый индекс $j_2$, чьё чётное значение равно $2j_1$, а нечётное равно $2j_1+1$. Его значения в совокупности равны $j_2=0,...,2^{n+1}-1$. Из этого, наконец, вытекает, что для разности справедлива оценка $f_{n+1}(\mbf{x})-f_n(\mbf{x})=\frac{i_2-1}{2^{n+1}}-\frac{i_1-1}{2^n}=\frac{2^{n+1}k+j_2-2(2^nk+j_1)}{2^{n+1}}=\frac{j_2-2j_1}{2^{n+1}}\ge0$.

2.
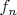
Пусть $O\subseteq[0,+\infty)$ -- произвольное открытое множество. Тогда по определению борелевской функции $f^{-1}(O)$ суть борелевское множество. Таким образом функции $f_n$ определены для всех $n\in\bb{N}$.

Пусть $f(\mbf{x})<n$, а для определённости $f(\mbf{x})\in[k+\frac{j}{2^n},k+\frac{j+1}{2^n})$ для каких-либо $k=0,...,n-1$ и $j=0,...,2^n-1$. Тогда $f(\mbf{x})-f_n(\mbf{x})<k+\frac{j+1}{2^n}-(k+\frac{j}{2^n})=\frac{1}{2^n}\to 0$ при $n\to\infty$, т.е. $f_n(\mbf{x}) \uparrow f(\mbf{x})$.

Если же $f(\mbf{x})\ge n$, то ввиду $\lfloor{f(\mbf{x})}\rfloor\le f(\mbf{x}) <\lfloor{f(\mbf{x})}\rfloor+1$ достаточно взять $N:=\lfloor{f(\mbf{x})}\rfloor+1+\lceil{-\log_2\varepsilon}\rceil$, чтобы каково бы ни было наперёд заданное $1>\varepsilon>0$, нашёлся номер $N$ такой, что для всех $n>N$ выполнялось $f(\mbf{x})-f_n(\mbf{x})=\frac{1}{2^n}<\varepsilon$. Значит, снова имеем $f_n(\mbf{x}) \uparrow f(\mbf{x})$.