RIPГлавный ультрафильтр, порожденный данным элементом
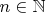
будет семейством надмножеств

из

. Хм.. , ну да,

получается.
Занятная задача получается, интересно.
-- Ср май 05, 2010 21:04:23 --Так... пусть

есть идеал из функций, для которых множество натуральных нулей принадлежит какому-то фиксированному ультрафильтру. Допустим, что он не максимальный и содержится в максимальном

.
Пусть

. Тогда множество ее натуральных нулей непусто (иначе рассматриваем

квадрат какой-то функции из

, обращающейся в ноль на

, получаем обратимый элемент )
Значит, у каждой такой функции

подмножество натуральных нулей непусто, и не принадлежит исходному ультрафильтру. Но нули функций из

образуют фильтр, мажорирующий исходный, противоречие?..
-- Ср май 05, 2010 21:12:09 --А, еще надо проверить аксиому про то, что надмножество любого элемента фильтра тоже лежит в фильтре.