Re: Мера Леви

[Gortaur]

Привет всем. помогите, пожалуйста. Есть процесс, чей дифур имеет вид:

$$ dX_t = A(t,X_t)dt+B(t,X_{t-})dN_t $$

где $N_t$ - пуассоновский процесс. Как для процесса $X$ найти jump measure или Levy measure?

[Хорхе]

В правой части Вашего уравнения русским языком написано, как найти, --- берем скачки пуассоновского процесса и растягиваем. Тут скачков немного, так что меру можно выписать:

$$ \sum_{t\in dt} (N_t - N_{t-}) \delta_{B(t,X_{t-})}(dx). $$

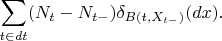
Естественно, чтобы получить явное выражение, уравнение придется решить.

(Надеюсь, я правильно понял, что именно требуется.)

(Оффтоп)

Что за странный глюк? Почему меня написали автором первого поста?