Полярные координаты - длина кривой.

[Legioner93]

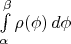
Никак не могу вывести длину кривой в полярных координатах. Где можно посмотреть вывод формулы? С подстановкой в параметрическую формулу в декартовых координатах $\int\limits_a^b \sqrt{{x'}^2(t) + {y'}^2(t)}\, dt$ все понятно, а вот вывести "напрямую" не могу. Приближая кривую дугами окружности или хордами, получается $\int\limits_\alpha^\beta\rho(\phi)}\,d\phi$, что, конечно, не верно. Спасибо!

[ewert]

Вывод вполне тривиален. Рассматриваем перемещение как гипотенузу бесконечно малого треугольничка, одним из катетов которого является смещение по радиусу, а вторым -- по координатной окружности. Моментально получаем $dl=\sqrt{(d\rho)^2+(\rho\,d\varphi)^2}$. И остаётся лишь вынести дифференциал угла за скобки и потом из-под корня.

[Полосин]

Или так: $r=r(\varphi)$, $x=r\cos\varphi$, $y=r\sin\varphi$, $x'=r'\cos\varphi-r\sin\varphi$, $y'=r'\sin\varphi+r\cos\varphi$, $x'^2+y'^2=r^2+r'^2$.

[ewert]

Именно так, если речь о формальном доказательстве. А если лишь о выводе -- то просто через теорему Пифагора.

[Legioner93]

Спасибо, разобрался!