, а как решать для квадратичной функции?
Не важно, для какой. Общая схема: пусть есть набор "узлов"

, "узловых значений"

. И надо приблизить эти данные линейными комбинациями вида

, где
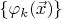
-- заданные функции, минимизируя сумму квадратов отклонений. Тогда набор чисел

-- это решение системы линейных уравнений

, где

и

.
У Вас

и

.