Проверьте пожалуйста решение:
Пусть

Доказать, что

.
Делаем чисто формально:

(Продолжаем со следующей строчки)

И далее уже понятно, что от первой суммы остается
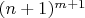
(последнее слагаемое), а от второй суммы

(это вклад всех единиц) и еще единица (первое слагаемое). И того ответ:
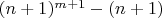
Вроде все формально правильно, но что-то сомнения есть в законности суммирования таким образом.
P.S. Задача из трехтомного сборника задач Кудрявцева, том 1, стр. 31, №15.