Ну не совсем так, как уважаемый профессор Снейп
А вот хотя бы так:
Если

и

находятся в отношении R, то есть

, то тогда
1) При любом

также

2) При любом

таком, что

также

И что неужели вообще невозможно такое отношение построить в поле комплексных чисел?
Вообще, раз употребляется термин "порядок", то хотелось бы, чтоб аксиомы порядка были выполнены. Хотя бы частичного.
Хотя вот пустое отношение --- строгий частичный порядок...
Давайте определимся со следующим: порядок должен быть линейным или допускаются несравнимые элементы?
Если допускаются, то пример с пустым отношением годится. Или, допустим, действительные числа сравнимы стандартно, а остальные только сами с собой, тоже пример.
Если же требуется линейность...
1) Для любого

либо

и

, либо

и

по той же самой причине.
2) Для любого

либо

и

, либо

и
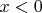
, согласно аналогичному аргументу.
3) Таким образом, для

ровно одно из двух чисел

больше нуля.
4) Для любого

имеем

.
5) Значит, имеем противоречие с

,

и

.
-- Сб фев 27, 2010 04:01:35 --Ну в общем то определение, которое привел Профессор Снэйп, эквивалентно тому, что отношение является линейным порядком + ваши две аксиомы.
Ага, есть такое.
-- Сб фев 27, 2010 04:05:25 --Грубо говоря, не выйдет ли так, что если в поле можно построить такое отношение, то оно обязательно совпадет с каким-нибудь полем, кольцом (ну или еще чем-то) от этого же, но действительных чисел с точностью до изоморфизма.
Чиво?