Условие единственности

[mihiv]

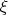
Задача связана с вопросом arseniv от 28.01.10. в разделе "Помогите решить..." о решении функционального уравнения $\xi \circ f=g\circ \xi \qquad (1)$В (1) $f$ и $g$ известные,а $\xi $-неизвестная функция.
Рассмотрим множество функций $[0,1]\to [0,1]$,для каждой из которых выполнено условие существования обратной функции.Считаем,что $f,g,\xi $ принадлежат этому множеству.Найти необходимое условие единственности решения уравнения (1).

[mihiv]

Т.к необходимое условие в принципе определено не однозначно ,то уточню условие задачи:доказать,что если уравнение (1) имеет единственное решение,то $f(f(x))=g(g(x))\equiv x.$

[nckg]

В случае $f=g$ всё довольно просто.
Решение уравнения $\xi f = f \xi$ всегда существует --- это $\xi = f^{-1}$.
Тогда из единственности имеем: $\xi f = f \xi$ $\Leftrightarrow$ $\xi = f^{-1}$.
Сама функция $f$ всегда является решением уравнения $\xi f = f \xi$, но тогда $f=f^{-1}$, т.е. $f f=e$.

-- Ср фев 17, 2010 11:32:37 --

А в случае $f\neq g$ решение такое:
$\xi f = g \xi$ $\Rightarrow$ $g \xi f f = g g \xi f$, то есть $\eta = g \xi f$ также будет решением уравнения $\eta f = g \eta$. В силу единственности $\xi = \eta$, то есть $\xi = g \xi f$.
Но из исходного уравнения имеем $\xi = g \xi f^{-1}$, откуда в силу обратимости элементов $f=f^{-1}$.
(Аналогично с $g$).

[mihiv]

nckg,да, все верно ,но пока задача была на форуме,я решил предложить еще одну задачу на тему этого уравнения:доказать,что если уравнение (1) имеет решение,то это решение не единственно.

[nckg]

Тогда продолжим. Пусть решение $\xi$ существует и единственно. Как было показано выше, тогда $\xi = g \xi f$, $f^{-1}=f$ и $g^{-1}=g$.
Обозначим $h=\xi f = g \xi$. Тогда

$$g h f = g \xi f f = g g \xi f,$$

$$g h f = \xi f = g \xi = h,$$

$$h f = g h,$$

то есть $h$ --- тоже решение уравнения (1). В силу предположенной единственности $h= \xi$, поэтому $\xi = \xi f = g \xi$, откуда $f = g = e$, после чего получаем противоречие.