Здравствуйте.
При решении некоторой задачки вылезло такое неравенство, хотел помыслить себе такую оценку:
![$\[\sum\limits_{n = 1}^N {n \cdot {n^\varepsilon }} > \sum\limits_{n = 1}^N {n \cdot {{\left( {Nk} \right)}^\varepsilon }} \]$ $\[\sum\limits_{n = 1}^N {n \cdot {n^\varepsilon }} > \sum\limits_{n = 1}^N {n \cdot {{\left( {Nk} \right)}^\varepsilon }} \]$](https://dxdy-04.korotkov.co.uk/f/3/1/4/314f2bc01f91c064f49641703ffc981482.png)
где
![$\[\varepsilon \in \left( {0,\frac{1}
{2}} \right)\]$ $\[\varepsilon \in \left( {0,\frac{1}
{2}} \right)\]$](https://dxdy-04.korotkov.co.uk/f/3/b/1/3b1eda086b0ca5b0998783689d01dd2182.png)
,
![$\[k \in \left( {0,1} \right)\]$ $\[k \in \left( {0,1} \right)\]$](https://dxdy-01.korotkov.co.uk/f/0/3/8/0383ab6e1c07076272bab59ac858cc7082.png)
при каких k это справедливо?
ну чисто интуитивно допустим
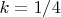
подходит.
ещё приходило в голову представить так:
![$\[\sum\limits_{n = 1}^N {n \cdot {x^\varepsilon }} \]$ $\[\sum\limits_{n = 1}^N {n \cdot {x^\varepsilon }} \]$](https://dxdy-02.korotkov.co.uk/f/9/3/1/93135ca8012f96f4c7a102e5e892905c82.png)
, продифференцировать по х и искать экстремумы при
![$\[x \in (1,N)\]$ $\[x \in (1,N)\]$](https://dxdy-04.korotkov.co.uk/f/7/a/4/7a4733211cdf755e630421bc83364beb82.png)
, но что-то в суммах запутался и непонятно, можно ли так делать,
подскажите, пожалуйста, что-нибудь?