Теорема Стотерса-Мейсона-Снайдера или ВТФ для многочленов

[Slava]

В статье В. В. Прасолова "Диофантовы уравнения для многочленов" есть интересная теорема:
Теорема 3. Пусть $f, g, h$ - взаимно простые многочлены, причем хотя бы один из них - не константа. Тогда равенство $f^n+g^n=h^n$ не может выполняться при $n\geqslant3$.
Она - аналог ВТФ для многочленов.
Ее можно легко обобщить:
Пусть $f_1, f_2, ...,f_{m-1}, f_m$ - взаимно простые многочлены, причем хотя бы один из них - не константа. Тогда равенство $f_1^n+f_2^n+...+f_{m-1}^n=f_m^n$ не может выполняться при $n\geqslant m$.
Доказательство. Согласно теореме Мейсона, степень каждого из многочленов $f_1^n, f_2^n, ...,f_{m-1}^n, f_m^n$ не превосходит $\deg f_1+\deg f_2+...+\deg f_m-1$.
Сложив эти $m$ неравенств, получим
$n(\deg f_1+\deg f_2+...+\deg f_m)\leqslant m(\deg f_1+\deg f_2+...+\deg f_m-1)$.
Следовательно, $n<m$.
Потом в этой статье автор доказал, что если рассматривать обобщенное уравнение
$f^{\alpha}+g^{\beta}=h^{\gamma}$, (*)
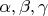
то для чисел $\alpha, \beta, \gamma$ возможны только такие наборы
$(2, 2, \gamma), (2, 3, 3), (2, 3, 4), (2, 3, 5)$. (**)
Также можно рассмотреть обобщенное уравнение
$f_1^{\alpha_1}+f_2^{\alpha_2}+...+f_{m-1}^{\alpha_{m-1}}=f_m^{\alpha_m}$ и сделать анализ показателей.
Теперь вопросы:
1) Можно ли обобщать теорему 3 и правильное ли доказательство обобщенной теоремы? (Автор этого не сделал)?
2) Если я правильно понял, то эта теорема помогает в параметризации диофантовых уравнений с помощью многочленов. Например для уравнения (*) известны параметризации для наборов показателей (**). Так ли это?
3) По этой теореме получается, что существует параметризация уравнения $x^4+y^4+z^4+t^4=u^4$ (если обобщенная теорема правильная). Почему тогда до сих пор ее не нашли?
4) Эта теорема должна называться Стотерса-Мейсона-Снайдера (по крайней мере так говорит Интернет). Почему автор назвал ее теоремой Мейсона.

[maxal]

Slava в сообщении #279975 писал(а):

3) По этой теореме получается, что существует параметризация уравнения $x^4+y^4+z^4+t^4=u^4$ (если обобщенная теорема правильная). Почему тогда до сих пор ее не нашли?

Попробуйте сами и расскажите нам "почему".