Последовательный запуск. Задача

[kkdil]

MOPO3OB в сообщении #284718 писал(а):

...кстати, если кто не понял, в стартовой ИСО расстояние между ракетами $L \rightarrow 0$ при $t \rightarrow \infty $.

....
Кстати. Кто не понял. Скорость света в СТО - константа... И предел...

[peregoudov]

А прикольно выглядит пост Морозова, повторяющий мой пост с цитатой. Чукча --- не читатель!

[kkdil]

peregoudov в сообщении #284732 писал(а):

:lol: А прикольно выглядит пост Морозова, повторяющий мой пост с цитатой. Чукча --- не читатель!

Данный чукча - ДеБилл...
Надеюсь, что выразил мнение масс...

ЗЫ. Настолько боится Морозов, что до сих пор блокирует на личном своем сайте, т.е. приватизированном, мои сообщения

[MOPO3OB]

Что-то Вы расшалились.... порядочностью тут не пахнет. Теперь знаю кто пишет и писает в лифтах....

Поскольку тема зафлужена форумной шпаной .... повторю решение:

MOPO3OB в сообщении #284718 писал(а):

В нерелятивистской кинематике последовательный пуск из одной точки равноускоренных ракет дает простой результат. Расстояние между ними увеличивается по линейному закону
$s=a(t+t_0)^2-at^2=2att_0+at_0^2 $
Предлагаю решить релятивистскую задачу.
___________________________________________
разумеется интересна асимптотика при $t\rightarrow\infty $
___________________________________________
последнее условие добавлено в расчете на ожидаемое тривиальное, но неверное решение
___________________________________________
Мне надоела болтовня.

Решение
Уравнение движения для точки (ракеты) №1 для $\tau\geq 0$
$x_1=\frac{c^2}{a} \cosh \frac{a\tau}{c}$
$ct_1=\frac{c^2}{a} \sinh \frac{a\tau}{c}$
Для точки №2 для $\tau\geq \tau_0$
$x_2=\frac{c^2}{a} \cosh \frac{a(\tau-\tau_0)}{c} $
$ct_2=\frac{c^2}{a} \sinh \frac{a(\tau-\tau_0)}{c}$
4-интервал между точками
$s^2=( ct_2- ct_1)^2-( x_2- x_1)^2$
$ s^2=\left( \frac{c^2}{a} \sinh \frac{a(\tau-\tau_0)}{c}- \frac{c^2}{a} \sinh \frac{a\tau}{c}\right)^2- $$ -\left( \frac{c^2}{a} \cosh \frac{a(\tau-\tau_0)}{c}- \frac{c^2}{a} \cosh \frac{a\tau}{c} \right)^2 $
или
$ s^2=\frac{4c^4}{a^2}\left[ \left( \cosh \frac{a(\tau-\tau_0/2)}{c}\ \sinh \frac{a\tau_0}{2c}\right)^2-\left( \sinh \frac{a(\tau-\tau_0/2)}{c}\ \sinh \frac{a\tau_0}{2c}\right)^2\right]= $$=\frac{4c^4}{a^2} \left( \sinh \frac{a\tau_0}{2c}\right)^2=\frac{2c^4}{a^2} \left( \cosh \frac{a\tau_0}{c}-1\right). $
Такой "парадокс". Не зависит "собственное" расстояние между ракетами от времени. это несмотря на то, что их скорости различны.
Такая вот простенькая задачка.
...кстати, если кто не понял, в стартовой ИСО расстояние между ракетами $L \rightarrow 0$ при $t \rightarrow \infty $.

[kkdil]

MOPO3OB в сообщении #284747 писал(а):

Что-то Вы расшалились....

Может быть.

MOPO3OB в сообщении #284747 писал(а):

порядочностью тут не пахнет.

Угу. За Вами таких запахов не замечалось. Все больше дерьмецом попахивает. Ничего личного, просто констатация фактов.

MOPO3OB в сообщении #284747 писал(а):

Теперь знаю кто пишет и писает в лифтах....

Морозов, конечно. Не велико открытие.

MOPO3OB в сообщении #284747 писал(а):

Поскольку тема загажена....

Угу. Морозов не один форум загадил...

[MOPO3OB]

Цитата:

ЗЫ. Настолько боится Морозов, что до сих пор блокирует на личном своем сайте, т.е. приватизированном, мои сообщения

Ложь! Гражданин начальник. Паранойя.
Уже год Вы трезвоните о происках Морозова. ... подленько все это, мелко. Я вам предлагал встретиться, давал телефон. Спрятались? голову в песок?
Традиционные вопли "забижают!" ..."любителей бьют!" ....тьфу на вас...

[kkdil]

MOPO3OB в сообщении #284751 писал(а):

Цитата:

ЗЫ. Настолько боится Морозов, что до сих пор блокирует на личном своем сайте, т.е. приватизированном, мои сообщения

Ложь! Гражданин начальник. Паранойя.
Уже год Вы трезвоните о происках Морозова. ... подленько все это, мелко. Я вам предлагал встретиться, давал телефон. Спрятались? голову в песок?

С Вами встречаться? Добровольно? Увольте, Вы слишком высокого мнения о себе. О чем с Вами разговаривать? О Вас великом ?

ЗЫ. И где два моих сегодняшних сообщения?

[MOPO3OB]

Цитата:

Постоянство указанного интервала представляет собой забавный математический курьез.

Верно. Я был не прав, считайте пошутил:

MOPO3OB в сообщении #284718 писал(а):

...кстати, если кто не понял, в стартовой ИСО расстояние между ракетами при .

Однако и тривиальное решение оказалось неверным. И Картинка конечно неверная. Конечно не в правилах перегудова говорить, что он был не прав.
В задаче интересно, что тут явно вмдно запись решения по-Белловски не имеет места быть.

-- Вс янв 31, 2010 17:40:23 --

Цитата:

ЗЫ. И где два моих сегодняшних сообщения?

Ой Я понял!
Вы просто не читаете названия кнопок на которые давите!
...я тоже на это покупаюсь.

Я знаю где ваши сообщения... Вы нехорошо себя ведете, но я сообщу Вам по секрету. Вы их СОХРАНИЛИ!
Личный раздел > Черновики
Я туда естественно не вхож и прочитать их не смогу....
Бережливость хорошее качество.

А встретиться я хотел что б рассказать Вам о задаче. На форуме это не очень эффективно. Другое дело при личном общении. По крайне мере в лицо гадости нормальный человек не говорит, как правило.

[MOPO3OB]

один идиот нарисовал хорду к гиперболе и и сказал, что это интервал s.
Я не собираюсь обсуждать ЭТУ глупость.

Задача с раздельным стартом интересна не тем, что ее решить правильно оказалось сложно для некоторых.
Интересно ее решение
При фиксированном 4-интервале в ИСО расстояние между ракетами неограниченно растет.
Никакого растяжения Белла и рваных трусов тросов.

[peregoudov]

Ну, мы тогда тоже наш разбор копипастнем

peregoudov в сообщении #283494 писал(а):

MOPO3OB в сообщении #283428 писал(а):

Меня ломает переиначивать формулы решения с форума на форум.

Морозова ломает копипастить? Вот уж не поверю! Требую рассматривать это как скрытую рекламу ФИАНовской помойки!

Давайте посмотрим, что же там пишет Морозов.
http://forum.lebedev.ru/viewtopic.php?p ... cc8#p33766

Цитата:

В нерелятивистской кинематике последовательный пуск из одной точки равноускоренных ракет дает простой результат. Расстояние между ними увеличивается по линейному закону

$$s=a(t+t_0)^2-at^2=2att_0+at_0^2$$

Предлагаю решить релятивистскую задачу.
___________________________________________
разумеется интересна асимптотика при $t\to\infty$
___________________________________________
последнее условие добавлено в расчете на ожидаемое тривиальное, но неверное решение
___________________________________________
Мне надоела нравоучительная болтовня.

Решение
Уравнение движения для точки (ракеты) №1 для $\tau\geq0$

$$x_1=\frac{c^2}a\mathop{\rm cosh}\frac{a\tau}c$$

$$ct_1=\frac{c^2}a\mathop{\rm sinh}\frac{a\tau}c$$

Для точки №2 для $\tau\geq\tau_0$

$$x_2=\frac{c^2}a\mathop{\rm cosh}\frac{a(\tau-\tau_0)}c$$

$$ct_2=\frac{c^2}a\mathop{\rm sinh}\frac{a(\tau-\tau_0)}c$$

4-интервал между точками

$$s^2=(ct_2-ct_1)^2- (x_2-x_1)^2$$

$$s^2=\left(\frac{c^2}a\mathop{\rm sinh}\frac{a(\tau-\tau_0)}c-\frac{c^2}a\mathop{\rm sinh}\frac{a\tau}c\right)^2-\left(\frac{c^2}a\mathop{\rm cosh}\frac{a(\tau-\tau_0)}c-\frac{c^2}a\mathop{\rm cosh}\frac{a\tau}c\right)^2$$

или

$$s^2=\frac{4c^4}{a^2}\left[\left(\mathop{\rm cosh}\frac{a(\tau-\tau_0/2)}c\mathop{\rm sinh}\frac{a\tau_0}{2c}\right)^2-\left(\mathop{\rm sinh}\frac{a(\tau-\tau_0/2)}c\mathop{\rm sinh}\frac{a\tau_0}{2c}\right)^2\right]=$$

$$=\frac{4c^4}{a^2}\left(\mathop{\rm sinh}\frac{a\tau_0}{2c}\right)^2=\frac{2c^4}{a^2}\left(\mathop{\rm cosh}\frac{a\tau_0}c-1\right)$$

Такой "парадокс". Не зависит "собственное" расстояние между ракетами от времени. это несмотря на то, что их скорости различны.
Такая вот простенькая задачка.
...кстати, если кто не понял, в стартовой ИСО расстояние между ракетами $L\to0$ при $t\to\infty$.

Цитата:

Мне надоела нравоучительная болтовня.

А уж как нам надоела нравоучительная морозовская болтовня! Я давно твержу: хватит надувать щеки, давайте сюда ваши глупости. Хвала Аллаху, мы дождались! Комментируем.

1. Морозов думает, что его "уравнения движения" описывают две ракеты. На самом деле никаких двух ракет у Морозова нету, оба уравнения для $(x_1,t_1)$ и $(x_2,t_2)$ описывают одна и ту же мировую линию, просто по-разному параметризованную: точка мировой линии, при первой параметризации соответствующая $\tau$, при второй соответствует $\tau+\tau_0$.

2. Морозов думает, что вычисляет какое-то одному ему ведомое "собственное расстояние между ракетами". На самом деле он вычисляет интервал между двумя точками на одной мировой линии. Этот интервал является времениподобным и как расстояние интерпретирован быть не может.

3. Всю эту глупость можно наглядно проиллюстрировать графически так

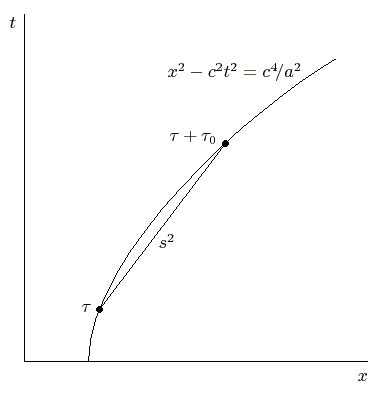
Постоянство указанного интервала представляет собой забавный математический курьез.

Кстати, тут Munin низвел морозовское "открытие" вообще до тривиальщины: оказывается, Морозов открыл, что хорда, стягивающая дугу окружности определенной величины, всегда имеет одну и ту же длину, где бы на окружности вы эту дугу ни брали.

[photon]

Флейм, оффтопик, оверквотинг, злоупотребление смайлами. Закрываю во избежание развития в том же духе.

kkdil, вам персонально неделя на изучение правил