Фундаментальная система окрестностей нуля

[twisty]

В бесконечномерном банаховом пространстве в слабой топологии нет счетной фундаментальной системы окрестностей нуля.

Обязательно бы написал свои идеи. Но, увы, их нет. Пожалуйста, подскажите, в каком направлении мыслить.

[nckg]

Думаю, что это можно доказать, используя следующие рассуждения:
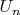
1) Если есть счётная фундаментальная система окрестностей нуля $U_n$ (а каждая окрестность нуля задаётся конечным набором функционалов), то есть счётная система полунорм, которая задаёт слабую топологию.
2) ЛВП метризуемо тогда и только тогда, когда оно отделимо и обладает счётным порождиющим набором полунорм. Поэтому наше б.п. со слабой топологией метризуемо (норму обозначим как $\|\cdot\|_w$).
3) Слабая топология бесконечномерного б.п. не является метризуемой.
3') или так: для любого $n\in \mathbb N$ найдётся $x_n\in X$, $\|x_n\|_w=1$, принадлежащий $\cap_{i=1}^n U_i$ (иначе X есть ядро конечного набора функционалов, задающих $U_i$, $i=1,...,n$, и поэтому конечномерно). Получили последовательность, которая по определению сходится к нулю, а по норме - нет.

см. также здесь.

[twisty]

Огромное спасибо!