The preceding discussion in section 2.6 sets a context for discussing
operator notations and analogies between finite and infinite calculus.
The same symbols
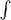
and
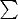
are used for operators that map
functions to functions and for operations that map functions to values;
disambiguation comes by using
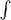
with
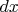
and
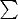
with
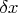
when the second interpretation is intended. Thousands of mathematicians
from Lagrange onwards have used the notations in this section successfully,
but of course many other conflicting notations also exist. Questions of
taste cannot be argued. I'm sure that you cannot convince me that your
favorite notation is better than mine, any more easily than I could
convince you that mine is what you should adopt. I will continue however to
do what I think is best (especially after liking it for forty years)!
I do not have time or energy to argue such things; I want to get work
done. I communicate my ideas in hopes that others will find them useful,
but if they don't see things my way I am not going to push. (Maybe that's why
Grothendieck is in hiding?) I certainly don't want to give up on
linear operators just because high-school students are traditionally
taught something else. Take a look at equation (9.70), which is
formally and conceptually very important. Concrete Math is my Manifesto.
Of course I don't change TeX every time a user complains either.
Похоже, меня немного не так поняли (я уже написал ответ), но самое важное тут сказано - для функции
и именно они имеются в виду в формулах интегрирования и суммирования по частям. К сожалению, я не нашел четкого определения