При игре в керлинг камни запускают по ледовой дорожке, причем коэффициент трения камня о лед можно менять, царапая лед скребком или полируя его щеткой. Коэффициент трения обычного(нетронутого) льда

, поцарапанный скребком лед имеет коэффициент трения

, а отполированный щеткой-коэффициент

. Камень запустили так, что он начал скользить со скоростью


. Что следует взять-скребок или щетку- и какую часть дорожки надо обработать, чтобы камень остановился на расстоянии

от точки удара? При каких скоростях

это вообще возможно?

Я решал эту задачу, пользуясь только вторым законом Ньютона, главными уравнениями кинематики и следствиями из них.
Сначала запишем дано:











1. Движение камня без использования щетки или камня.
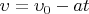

Отсюда

и

Из второго закона Ньютона

, следовательно при данных параметрах движения тело выполнит условия задачи при движении по льду с коэффициентом трения

, а у нас 0.04.
2.Так как нам нужно понизить коэффициент трения, то мы будем использовать щетку. Вопрос какую часть пути полировать?
Предположим, что

- участок пути, на котором тело будет двигаться по обычному льду, а

- по отполированному.

При известных коэффициентах трения, ускорением свободного падения, начальной скорости 1 этапа и конечной второго найдем ускорения для каждого из этапов движения.



.


. Так как


, а

.
При подстановке получаем, что

Это невозможно. При начальной скорости 3 - 33 м, а нам нужно 3,3, следовательно начальная скорость должна быть в 10 раз меньше - 0,3 м/с.
Тогда часть льда, которую нужно отполировать будет иметь протяженность 6,7 м.
Ответ: щетку, 6,7 м, при скорости в 10 раз меньше данной.
Верно ли я решил задачу?