МП-автомат для распознавания заданного языка

[MMM-2000]

Необходимо построить МП-автомат который распознает язык $L$
где $L=\{\alpha$#$\beta | \alpha, \beta \in A^{*} ; |A|=2; \alpha \neq \beta\}$
где $A$ - алфавит
# - не принадлежит этому алфавиту

Проблема в следующем:
При чтении слова альфа я записываю его на ленту до тех пор пока не встречу символ #
после этого в стеке автомата слово $\alpha$ лежит как бы перевернутое и возникает проблема при сравнении слова $\alpha$ и $\beta$
(так как на каждом шаге мы видим только одну букву с вершины стека)

У меня две идеи: каким-то образом записывать стек перевернутым или каким-то образом сравнивать слова так как есть после записи первого в стек.

Первую я не представляю как реализовывать.
А если сравнивать в лоб, то есть идея задействовать булеву алгебру (алфавит не зря же по мощности равен двум), но пока не удалось с помощью операций выявить критерий равенства слов.

Подскажите пожалуйста, хотя бы в каком направлении лучше двигаться.

[Профессор Снэйп]

У меня такое ощущение, что этот язык вообще не будет контекстно-свободным.

[MMM-2000]

Если откинуть условие $\alpha \neq \beta$ то он не будет контекстно свободным это понятно.
А с этим условием у меня тоже возникала мысль о не контекстно свободности, но задание так стоит.
И лемму о разростании мне не удалось применить (если пытаться строить через КС грамматики) ни с помощью не замкнутости по операциям.

[Профессор Снэйп]

MMM-2000 в сообщении #269577 писал(а):

Если откинуть условие $\alpha \neq \beta$ то он не будет контекстно свободным это понятно.

Да Вы что? Если откинуть это условие, он будет ваще регулярным!!!

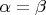
Вот если заменить это условие на "противоположное" условие $\alpha = \beta$, то он точно не будет контекстно-свободным и это легко доказывается. А с неравенством... не знаю.

-- Чт дек 10, 2009 00:55:41 --

Стоп! Кажется понял. Язык, конечно же, будет контекстно-свободным (но не детерминированно контекстно-свободным).

Автомат, естественно, должен быть недетерминированным и для распознавания он должен угадывать, какая по счёту буква в словах $\alpha$ и $\beta$ различаются (либо угадывать тот факт, что это слова разной длины, но сие вообще тривиально). До этой буквы всё пихаем в стек. Затем пропускаем остаток слова $\alpha$ вплоть до символа #. Затем снимаем верхнюю букву из стека и запоминаем её через состояние. Затем освобождаем стек, читая слово $\beta$ буква за буквой, и когда дойдём до нужной буквы (узнаём это по тому факту, что стек освободился), фиксируем различие и радуемся

-- Чт дек 10, 2009 01:17:12 --

Автомат рисовать не буду, поскольку полные решения запрещены правилами форума, но грамматику --- пожалуйста. Считаем, что $A = \{ a,b \}$.

$S \to aL | bL | Ra | Rb | M$
$L \to aL | bL | aLa | aLb | bLa | bLb | \sharp$
$R \to Ra | Rb | aRa | aRb | bRa | bRb | \sharp$
$M \to UX | VY$
$U \to aUa | aUb | bUa | bUb | aZ\sharp$
$V \to aVa | aVb | bVa | bVb | bZ\sharp$
$X \to bZ$
$Y \to aZ$
$Z \to aZ | bZ | \varnothing$

-- Чт дек 10, 2009 01:22:10 --

MMM-2000 в сообщении #269566 писал(а):

А если сравнивать в лоб, то есть идея задействовать булеву алгебру

Вот эти Ваши слова для меня вообще загадочны. Как Вы собирались какую-то булеву алгебру задействовать, даже не представляю.

[MMM-2000]

Профессор Снэйп в сообщении #269589 писал(а):

MMM-2000 в сообщении #269577 писал(а):

Если откинуть условие $\alpha \neq \beta$ то он не будет контекстно свободным это понятно.

Да Вы что? Если откинуть это условие, он будет ваще регулярным!!!

Прошу прощения за такую глупость. Я это впринципе имел ввиду но не написал. виноват.
ну то что $\alpha = \beta$


С грамматикой я разобрался, спасибо большое!
Автомат сам разумеется построю. =)
Еще раз спасибо.

з.ы.

Профессор Снэйп в сообщении #269589 писал(а):

Вот эти Ваши слова для меня вообще загадочны. Как Вы собирались какую-то булеву алгебру задействовать, даже не представляю.

Я подумывал о том что если считать $a=0$ и $b=1$ то как-то можно с помощью серии операций над буквами(как над числами) выяснить равенство слов.