3. Первообразная и неопределенный интеграл 3.1. Основные определения. Функция

называется первообразной функции

на промежутке

(конечном или бесконечном), если функция

непрерывна на

и

во всех внутренних точках.
Неопределенным интегралом от функции

на промежутке

называют, и обозначают

, множество всех первообразных:
 3.2. Свойства неопределенного интеграла.
3.2. Свойства неопределенного интеграла. Если функция

имеет первообразную на промежутке

, то для внутренних точек промежутка

Если функция

непрерывна па промежутке

и дифференцируема в его внутренних точках, то

Если функция

имеет первообразную на промежутке

, а

— число, то для функции

существует первообразная и

Если функции

и

имеют первообразные на промежутке

, то функция

также имеет первообразную и
![$$\int[f(x)+g(x)] dx=\int f(x) dx + \int g(x) dx.$$ $$\int[f(x)+g(x)] dx=\int f(x) dx + \int g(x) dx.$$](https://dxdy-04.korotkov.co.uk/f/f/c/d/fcdfe470ca36b2a900ac70f563d5bdc182.png) Интегрирование по частям.
Интегрирование по частям. Если функции

и

непрерывны на промежутке

, дифференцируемы в его внутренних точках и существует интеграл

, то на

существует и интеграл

и
 Интегрирование подстановкой (замена переменной).
Интегрирование подстановкой (замена переменной). Если функция

определена и имеет
первообразную на промежутке

, а функция

непрерывна на промежутке

, дифференцируема в его внутренних точках и

, то функция

имеет первообразную на

и
 3.3. Некоторые неопределенные интегралы от элементарных функций.
3.3. Некоторые неопределенные интегралы от элементарных функций. 
(в последнем интеграле промежуток интегрирования не содержит

); постоянную

всюду опускаем;

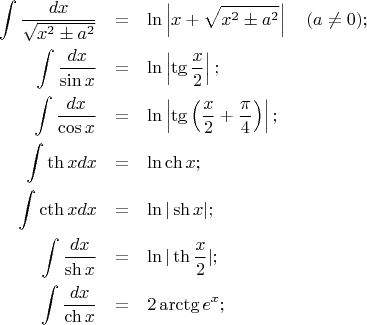 4. Некоторые неопределенные интегралы 4.1. Интегралы от рациональных функций
4. Некоторые неопределенные интегралы 4.1. Интегралы от рациональных функций. Интегралы, содержащие

.
![\begin{eqnarray*}
\int X^n dx&=&\frac{1}{a(n+1)}X^{n+1}\qquad(n\neq -1);\\
\int \frac{dx}{X}dx&=&\frac{1}{a}\ln|X|;\\
\int \frac{x dx}{X}&=&\frac{x}{a}-\frac{b}{a^2}\ln|X|;\\
\int \frac{x dx}{X^2}&=&\frac{b}{a^2 X}+\frac{1}{a^2}\ln|X|;\\
\int \frac{x dx}{X^n}&=&\frac{1}{a^2}\left(\frac{-1}{(n-2)X^{n-2}}+\frac{b}{(n-1)X^{n-1}}\right)\quad (n\neq 1,2);\\
\int \frac{x^2 dx}{X}&=&\frac{1}{a^3}\left(\frac{1}{2}X^2-2bX+b^2\ln|X|\right);\\
\int \frac{x^2 dx}{X}&=&\frac{1}{a^3}\left(\frac{1}{2}X^2-2bX+b^2\ln|X|\right);\\
\int \frac{x^2 dx}{X^2}&=&\frac{1}{a^3}\left(X-2b\ln|X|-\frac{b^2}{X}\right);\\
\int \frac{x^2 dx}{X^3}&=&\frac{1}{a^3}\left(\ln|X|+\frac{2b}{X}-\frac{b^2}{2X^2}\right);\\
\int \frac{x^2 dx}{X^n}dx&=&\frac{1}{a^3}\left[\frac{-1}{(n-3)X^{n-3}}+\frac{2b}{(n-2)X^{n-2}}-\frac{b^2}{(n-1)X^{n-1}}\right]\qquad (n\neq 1,2,3);\\
\int \frac{dx}{xX}&=&-\frac{1}{b}\ln\left|\frac{X}{x}\right|;\\
\int \frac{dx}{xX^2}&=&-\frac{1}{b^2}\left(\ln\left|\frac{X}{x}\right|+\frac{ax}
{X}\right);\\
\int \frac{dx}{xX^n}&=&-\frac{1}{b^n}\left[\ln\left|\frac{X}{x}\right|-\sum\limits_{i=1}^{n-1}C^i_{n-1}\frac{(-a)^i x^i}{iX^i}\right]\qquad (n\geq 1);\\
\int \frac{dx}{x^2X}&=&-\frac{1}{bx}+\frac{a}{b^2}\ln\left|\frac{X}{x}\right|;\\
\int \frac{dx}{x^2X^2}&=&-a\left[\frac{1}{b^2X}+\frac{1}{ab^2x}-\frac{2}{b^3}\ln\left|\frac{X}{x}\right|\right];\\
\int \frac{dx}{x^2X^n}&=&-\frac{1}{b^{n+1}}\left[\sum\limits_{i=2}^n C^i_n \frac{(-a)^{i-1}x^{i-1}}{(i-1)X^{i-1}}+\frac{X}{x}-na\ln\left|\frac{X}{x}\right|\right]\qquad(n\geq 2);\\
\int \frac{dx}{x^mX^n}&=&-\frac{1}{b^{m+n-1}}\sum\limits_{i=0}^{m+n-2} C^i_{m+n-2} \frac{X^{m-i-1}(-a)^i}{(m-i-1)x^{m-i-1}};\\
\end{eqnarray*} \begin{eqnarray*}
\int X^n dx&=&\frac{1}{a(n+1)}X^{n+1}\qquad(n\neq -1);\\
\int \frac{dx}{X}dx&=&\frac{1}{a}\ln|X|;\\
\int \frac{x dx}{X}&=&\frac{x}{a}-\frac{b}{a^2}\ln|X|;\\
\int \frac{x dx}{X^2}&=&\frac{b}{a^2 X}+\frac{1}{a^2}\ln|X|;\\
\int \frac{x dx}{X^n}&=&\frac{1}{a^2}\left(\frac{-1}{(n-2)X^{n-2}}+\frac{b}{(n-1)X^{n-1}}\right)\quad (n\neq 1,2);\\
\int \frac{x^2 dx}{X}&=&\frac{1}{a^3}\left(\frac{1}{2}X^2-2bX+b^2\ln|X|\right);\\
\int \frac{x^2 dx}{X}&=&\frac{1}{a^3}\left(\frac{1}{2}X^2-2bX+b^2\ln|X|\right);\\
\int \frac{x^2 dx}{X^2}&=&\frac{1}{a^3}\left(X-2b\ln|X|-\frac{b^2}{X}\right);\\
\int \frac{x^2 dx}{X^3}&=&\frac{1}{a^3}\left(\ln|X|+\frac{2b}{X}-\frac{b^2}{2X^2}\right);\\
\int \frac{x^2 dx}{X^n}dx&=&\frac{1}{a^3}\left[\frac{-1}{(n-3)X^{n-3}}+\frac{2b}{(n-2)X^{n-2}}-\frac{b^2}{(n-1)X^{n-1}}\right]\qquad (n\neq 1,2,3);\\
\int \frac{dx}{xX}&=&-\frac{1}{b}\ln\left|\frac{X}{x}\right|;\\
\int \frac{dx}{xX^2}&=&-\frac{1}{b^2}\left(\ln\left|\frac{X}{x}\right|+\frac{ax}
{X}\right);\\
\int \frac{dx}{xX^n}&=&-\frac{1}{b^n}\left[\ln\left|\frac{X}{x}\right|-\sum\limits_{i=1}^{n-1}C^i_{n-1}\frac{(-a)^i x^i}{iX^i}\right]\qquad (n\geq 1);\\
\int \frac{dx}{x^2X}&=&-\frac{1}{bx}+\frac{a}{b^2}\ln\left|\frac{X}{x}\right|;\\
\int \frac{dx}{x^2X^2}&=&-a\left[\frac{1}{b^2X}+\frac{1}{ab^2x}-\frac{2}{b^3}\ln\left|\frac{X}{x}\right|\right];\\
\int \frac{dx}{x^2X^n}&=&-\frac{1}{b^{n+1}}\left[\sum\limits_{i=2}^n C^i_n \frac{(-a)^{i-1}x^{i-1}}{(i-1)X^{i-1}}+\frac{X}{x}-na\ln\left|\frac{X}{x}\right|\right]\qquad(n\geq 2);\\
\int \frac{dx}{x^mX^n}&=&-\frac{1}{b^{m+n-1}}\sum\limits_{i=0}^{m+n-2} C^i_{m+n-2} \frac{X^{m-i-1}(-a)^i}{(m-i-1)x^{m-i-1}};\\
\end{eqnarray*}](https://dxdy-02.korotkov.co.uk/f/1/2/c/12c5cd16d82a012a62ef1cbd5077736082.png)
если

, то соответствующий член под знаком суммы заменяется членом

.