Здравствуйте. Сам решал, не могу решить. Может, сообщество поможет. Задача по вариационному исчислению.
Есть интеграл вида:
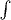
ẋḣtdt. x, h и t зависят от t. Причем ẋ означает, что функция x(t) была продифференцирована по t один раз (можно записать ẋ(t) = x'(t)). А интегрировать данную функцию можно лишь до состояния x(t). Далее можно заменить x на

и интегрировать дальше. h(t) можно интегрировать лишь до h. Брать интеграл

нельзя, нужно оставлять в данном виде. t можно интегрировать как обычную переменную от t.
Может кто сможет решить эту задачку...
П.С. Может кто знает формулу интегрирования произведения трех зависимых от одной переменной. То есть

. Очень помогла бы.