Dim1980 писал(а):
Так существует пример бесконечно-гладкой неаналитической функции?
Обозначим

Эта функция имеет на всей числовой оси производные всех порядков, и все производные ограничены (разными константами).
Точка

является особой для этой функции на комплексной плоскости, а формальный ряд Тейлора в точке

имеет вид

и не сходится к этой функции ни на каком интервале.
Пусть

- последовательность всех рациональных чисел. Тогда функция
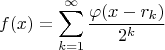
является искомой. Сам этот ряд и ряды, полученные из него почленным дифференцированием, мажорируемы, и потому абсолютно и равномерно сходятся. Поэтому

имеет производные всех порядков. Эта функция не разлагается в степенной ряд ни на каком интервале, так как множество её особых точек содержит все рациональные числа и, следовательно, всюду плотно на числовой прямой (напомню, что радиус сходимости степенного ряда по степеням

равен расстоянию от

до множества особых точек функции на комплексной плоскости).