Найти все а, при которых неравенство
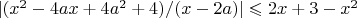
имеет хотя бы одно решение
Первую часть я преобразовала, получилось

Дальше нужно доказать, что левая часть не меньше четырёх, а правая - не больше четырёх. Вот это не очень понятно, почему именно четырех?
Спасибо заранее за помощь