Известна следующая теорема (см. Никольский, "Приближение функций многих переменных и теоремы вложения", стр 177):

В частности, отсюда при
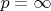
следует, что функция

, удовлетворяющая на интервале

условию Липшица с константой

имеет п.в. производную, причём
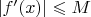
.
Вопрос: существует ли п.в. производная у функции

, удовлетворяющей на интервале

условию Гёльдера с константой

и показателем
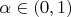

Вот
здесь утверждается, что вообще говоря нет, но пример не приводится:
Цитата:
Is it possible to relate this in some way(atleast partially) to the
sup|f'(x)|? (seems like this is probably the case but not completely sure
the connection)
Yes and no. There is certainly a connection between Holder
continuity and differentiability; in fact sort of the point
to those Holder conditions is that they give a _finer_ measure
of smoothness:
Let's say Lip_a is the set of functions satisfying a uniform
Holder condition of order a. If f is in Lip_1 then it turns
out that f is almost−everywhere differentiable, and in fact
the sup of |f'| is equal to the best constant in the Holder
condition. There is a converse to that, under slightly
more technical hypotheses.
Otoh f in Lip_a for a < 1 does not imply that f is differentiable.
So we have these two smoothness conditions, "continuous" and
"differentiable". Lots of functions in between, continuous
but not differentiable. Saying what Holder condition a function
satisfies gives a way of saying that one function is _closer_
to the differentiable range of the spectrum. Sort of.
-- Добавлено Thursday, September 24 2009, 07:25 PM --В книге Зигмунда "Тригонометрические ряды" (том 1, стр. 82) утверждается, что при любом
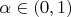
функция Вейерштрасса принадлежит
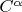
. Но в то же время она нигде не дифференцируема.