Не совсем уловил.
Возможно, потому, что я неграмотно записал. Имелось в виду: в достаточно малой окрестности этой предельной точки градиент мало меняется и, следовательно, существует некоторое гарантированное уменьшение целевой функции для любого приближения, попавшего в
несколько меньшую окрестность (ну например ровно вдвое меньшую).
Конкретнее. Допустим, в самой предельной точке модуль градиента есть

. Тогда в некоторой окрестности радиуса
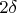
отклонение градиента от своего центрального значения не превысит по модулю

. Тогда для любых точек, попадающих в окрестность радиуса

, гарантировано уменьшение на следующем шаге не менее чем на

(поскольку расстояние от любой точки из окрестности радиуса

до границы окрестности радиуса
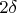
уж никак не меньше самой

).