Помогите доказать неравенство

для
![$f \in C([a, b])$ $f \in C([a, b])$](https://dxdy-02.korotkov.co.uk/f/5/6/2/5628de342e5930c1a1b019e4f83e95c682.png)
и такой, что
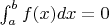
.
Здесь
![$m := -min_{[a, b]}f, M := max_{[a, b]}f$ $m := -min_{[a, b]}f, M := max_{[a, b]}f$](https://dxdy-04.korotkov.co.uk/f/b/f/5/bf557452b754c3c2fb8e4b8aafe1694082.png)
.
Я пробовал провести геометрическое доказательство и свёл это неравенство к такому, в котором слева площадь под той частью графика функции, где она больше

, а справа площадь прямоугольника высоты

, но для его основы не удалось придумать никакой подходящей оценки. Что делать дальше, неясно.
Заранее спасибо за помощь.