Тем кто забыл, что такое
поризм Понселе:
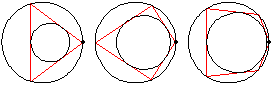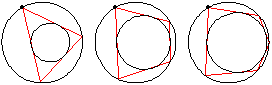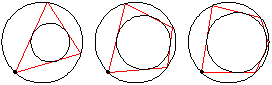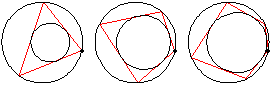 Summary этой заметки: если в поризме Понселе поменять местами R и d, ломаная всё равно замкнётся -- иногда за то же, иногда за вдвое большее, иногда за вдвое меньшее число шагов.
Summary этой заметки: если в поризме Понселе поменять местами R и d, ломаная всё равно замкнётся -- иногда за то же, иногда за вдвое большее, иногда за вдвое меньшее число шагов.Начнём с примера. Возьмём две окружности радиусов R=8 и r=3, расстояние между центрами которых равно d=4. Эти две окружности удовлетворяют теореме Понселе для n=3, т.е. существуют треугольники, вписанные во внешнюю окружность и описанные около внутренней. В качестве вершины треугольника можно взять любую точку внешней окружности.

Поменяем теперь R и d местами, т.е. построим отдельный чертёж с окружностями радиусов 4 и 3, расстояние между центрами которых равно 8. Оказывается, новые окружности удовлетворяют поризму Понселе для n=6! Шестиугольник получается самопересекающийся, но всё равно -- для любой точки окружности радиуса 4 цепочка касательных замкнётся за
6 шагов.
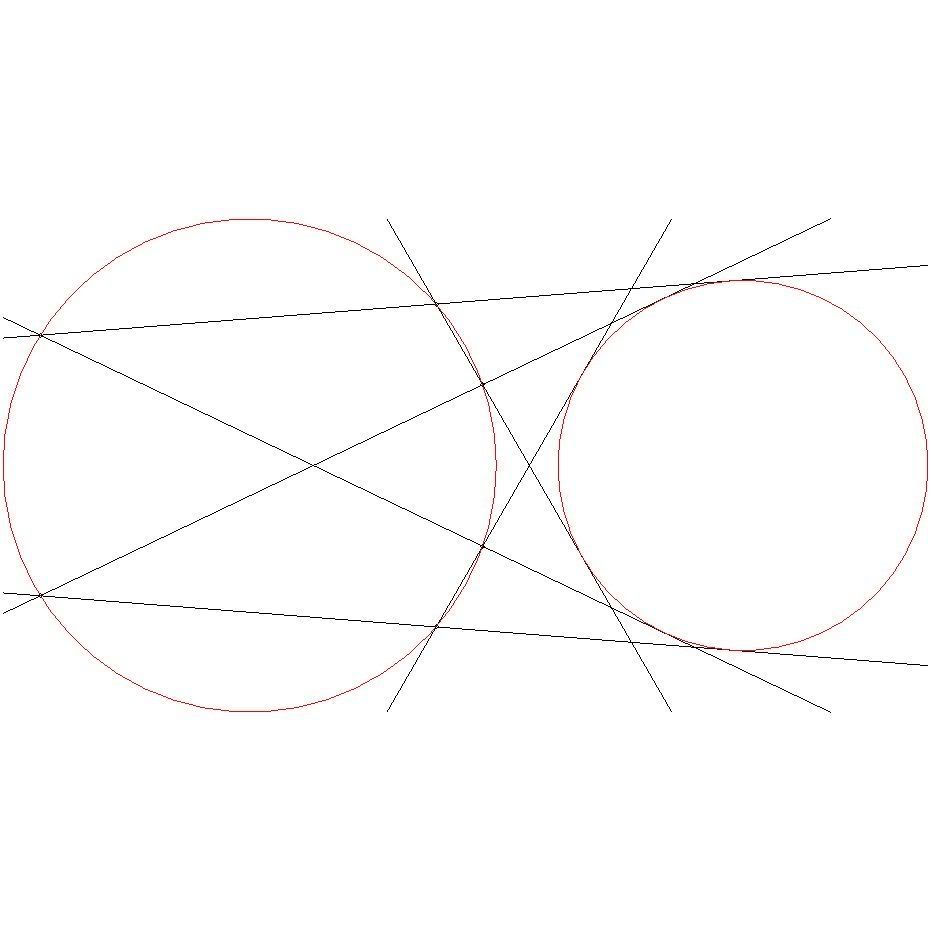
При чётном n замена R и d также возможна. Новая цепочка замыкается иногда за n загов, иногда за n/2 шагов.
У меня есть доказательства, что R можно менять на d при n=3,4,5,6,7,8 (с полной классификацией -- в каких случаях в новой картинке число шагов в ломаной будет вдвое больше, в каких вдвое меньше, в каких то же). Предполагаю, что R можно менять на d при любом n. Доказательством не располагаю.
Если у кого-то есть идеи, напишите, пожалуйста, мне было бы интересно обсудить.
Картинки при других n можно посмотреть тут:
http://community.livejournal.com/ru_math/721777.htmlСпасибо!
С уважением,
Сергей Маркелов