похоже что да, т.к. преобразование фурье будет линейным ограниченным (и след-но непрерывным) оператором, см.
неравенство Хаусдорфа-Юнга (там правда рассматривается немного другой случай, но по-моему аналогичные выкладки можно и в Вашей задаче сделать) (если я правильно понял,
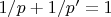
)
вопрос то не в этом. вопрос является ли преобразование Фурье отображением "на" -- нет не является, как мне тут объяснили:
No.
Hmm, there are probably cleaner ways to see this:
First, you can use the Rudin-Shapiro polynomials to
construct a continuous function on the circle such that
its Fourier coefficients do not lie in l^p for any p < 2.
(See for example the end of Chapter 23 in "Complex
Made Simple", heh-heh.)
I'm pretty sure it actually _follows_ that there exists
a function f on the line, continuous with compact
support, such that the Fourier transform f^ does
not lie in L^p for any p < 2. If we can't figure out
how the follows from the above, it certainly follows
by a similar argument to the one that proves the above.
Now f is in L^p' but there is no g in L^p with f = g^.
The reason being that, for example, there _is_
a tempered distribution g with f = g^ (g is the
reflection of f^), and g is not in L^p; uniqueness
for the Fourier transform for tempered
distributions shows that there is no such
g.
David C. Ullrich