обобщенно-однородные уравнения

[Ashley]

упражнение и совет из задачника А.Ф.Филиппова по диффурам.

Цитата:

Порядок уравнения понижается, если оно <...> не меняется от замены $x$ на $kx$, $y$ на $k^my$ (при этом $y'$ заменяется на $k^{m-1}y'$, $y''$ - на $k^{m-2}y''$ и т.д.).
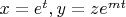
После того, как число $m$ найдено, надо сделать замену переменных $x = e^t, y = ze^{mt}$. Получим уравнение, в которое не входит независимое переменное $t$.

Понизить порядок, пользуясь однородностью: $x^3y''=(y-xy')(y-xy'-x)$

"$m$" $=1$, так??
но если $y=ze^t$, то $y' = e^t(z+z')$
если применять правило так, как я пытаюсь, то оно выглядит безумным
помогите разобраться

[ShMaxG]

Хм, весьма распространенная ошибка, кстати. Надо помнить, что $z=z(t)$, зависит от $t$, а не $x$. Поэтому и не получается ничего.

-- Вт июн 30, 2009 18:42:56 --

Ну т.е. в сам диффур входят производные игрека по иксу, их надо выразить через производные по $t$. Делается это так: $\[ \frac{{dy}} {{dx}} = \frac{{\left( {dy/dt} \right)}} {{\left( {dx/dt} \right)}} \] $.
Аналогично для второй производной.

[Ashley]

спасибо, точно, стыдно

[ShMaxG]

"В науке признание ошибки не считается позором" (из к/ф "Иду на грозу").