мажоранты задач о неподвижной точке

[terminator-II]

красивый результат принадлежащий Канторовичу.

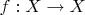
пусть $f:X\to X$ -- сильно дифференцируемое во всех точках отображение банахова пространства.
предположим, что существует такая точка $x_0\in X$ и такая $C^1$-функция $\psi:[t_0,T]\to \mathbb{R}$, что
1) $\|f(x_0)-x_0\|\le \psi(t_0)-t_0$
2) $\|f'(x)\|_{B(X)} \le\psi'(t)$ для всех $x$ и $t\in[t_0,T]$ таких, что $\|x-x_0\|\le t-t_0$. ($\|f'(x)\|_{B(X)}$ -- операторная норма)
доказать, что если отображение $\psi$ имеет неподвижную точку то и $f$ имеет неподвижную точку.