Опять несобственный интеграл

[Sonic86]

Вычислить $\int\limits_0^{+ \infty} \frac{x^2}{e^x+1}dx$.

[ИСН]

Такие обычно вкуснее всего раскладывать в ряд по степеням экспоненты.

[shwedka]

Градштейн и Рыжик,
3.411

[Sonic86]

ИСН писал(а):

Такие обычно вкуснее всего раскладывать в ряд по степеням экспоненты.

Это так что ли?:

$$\int\limits_0^{+ \infty} \frac{x^m}{e^x+1}dx = m! \sum\limits_{k=1}^{+ \infty} \frac{(-1)^{k-1}}{k^{m+1}}$$

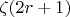
Получается, что при $m=2r$ интеграл выражается через $\zeta (2r+1)$. Тогда понятно, почему я его найти не могу.

schwedka писал(а):

Градштейн и Рыжик, 3.411

Спасибо будем читать.