Выясним, что такое время в ТО.

[igorelki]

Все 20 аксиом геометрии не дают разрезанности прямой по бесконечно удаленной точке.
Как у нас строятся координаты?
Берут точку 0 , берут точку 1, берут бесконечно удаленную точку. Затем по гармоническому соотношению (так называемое сложное отношение четырех точек) находят точку 2. И т.д. Так мы строим проективные координаты. Далее нам необходимо арифметизировать точки, расположенные на бесконечно удаленной плоскости. Для этого вводят дополнительную координату, которая дает однородность координатам. Выглядит это так:
Неоднородные координаты X,Y,Z добавляем координату $t$, причем x,y,z - однородные координаты и:
X=\frac{x}{t}
Y=\frac{y}{t}
Z=\frac{z}{t}
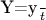
Таким образом, мы арифметизировали все пространство, включая бесконечно удаленную точку (это при t=0).
Чтобы задать размер необходимо иметь инвариант двух точек – что в народе называют интервалом. Тогда уже эти однородные координаты имеют преобразования, которые входят в ортогональную группу, а далее уже все автоматом – ПЛ.
А что там навыдумывали про время некоторые, не имеет основания.

Если есть вопросы, то ссылка на ВУЗовский учебник по математике
Н.В. Ефимов "Высшая геометрия", там большой объем, поэтому, если интересует конкретный вопрос, то дам ссылку.

[Коровьев]

igorelki в сообщении #220253 писал(а):

А что там навыдумывали про время некоторые, не имеет основания.

А что же там такое наповыдумывали про время некоторые, которое не имеет основания?
Хотелось бы знать.

[AD]

А мне интереснее, какие могут быть основания у того, что написано тут.
Это же обычная математика. Про окружающую действительность она ничего не утверждает.

[photon]

Не вижу физики, не вижу правильно оформленных формул, едем в карантин