Помогите разобраться с квадратичной форма

[Voodoo Man]

Задача такая:
Пусть квадратичная форма $h(X)$ - сумма элементов побочной диагонали матрицы $X^2$,$X \in \mathbb{R}^{n\times n}$. Найти её канонический вид и матрицу перехода к каноническому базису

Если матрица $X = ( x_{ij})$, где $x_{ij}$ - коэффициенты при базисном векторе $e_{ij}$ в некотором исходном базисе, то квадратичная форма записывается как

$$ \sum_{i=1}^{n} \sum_{j=1}^{n} x_{i,j} \cdot x_{j, n-j+1}$$

Произвольный элемент $x_{a,b}$ обладает следующим свойством : он встречается ровно в двух произведениях из $n^2$, а именно в $x_{a,b} \cdot x_{b,n+1-a}$ и $x_{a,b} \cdot x_{n+1-b,a}$
Квадрат среди этих произведений появляется только в случае, когда $n$ - нечётное, и при этом он ровно один : это $x_{\frac{n+1}{2},\frac{n+1}{2}} \cdot x_{\frac{n+1}{2},\frac{n+1}{2}}}$

Собственно говоря, узнав всё это, я пытаюсь применить метод Лагранжа, переписав немного вид исходной суммы как

$$\sum_{(i,j)}^{(i,j)\in n\times n} x_{i,j} \cdot x_{j, n-j+1} $$

Беру например произведение $x_{1,1} \cdot x_{1, n}$ (пока для случая $n$ чётного) и собираюсь делать стандартную замену; из всех слагаемых эта замена затронет ровно три : $x_{1,1} \cdot x_{1, n}$, $x_{n,1} \cdot x_{1, 1}$ и $x_{1,n} \cdot x_{n, n}$. Что и записываю, выкинув из $(i,j)\in n\times n$ все наборы приводящие к этим слагаемым:

$$\sum_{(i,j)}^{(i,j)\in n\times n \setminus (1,1), (n,1),(1,n)} (x_{i,j} \cdot x_{j, n-j+1} )+ x_{1,1} \cdot x_{1, n} + x_{n,1} \cdot x_{1, 1}+x_{1,n} \cdot x_{n, n}$$

(ну и далее применяю метод Лагранжа)
На первой итерации способ довольно удачный, но я до конца не уверен, проработает ли он на второй и до победного?

Другие идеи были :
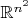
- Ввести "линейную" нумерацию через изоморфизм из $\mathbb{R} ^{n\times n}$ в $\mathbb{R}^{n^2}$ - пока ни к чему кроме упрощённой нумерации не привело;
- $h(X)$ есть след матрицы $X^2$ умноженной на матрицу, у которой все элементы нули, а на побочной диагонали - единицы;

Собственно говоря, если кто-то что-то может подсказать - поделитесь идеями....

[terminator-II]

действуйте по аналогии с topic22404.html
решение во втором посте

[Voodoo Man]

Cпасибо за помощь!