Как бы найти такой
неприводимый в поле
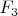
полином третьей степени, чтобы его корень являлся
образующей в группе

?
Среди неприводимых в
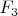
полиномов мне удалось найти два:

и

Как я понимаю, чтобы корень полинома был образующей в

достаточно чтобы

и вроде как такое число должно быть наименьшим.

В случае с

начинаю вычислять следующим образом:



и так далее (все коэффициенты привожу по модулю 3)
в итоге дохожу до

а должно было быть -1 (если бы корень являлся образующей, так как

)
Может, есть другие способы или я что-то неправильно делаю?