Теорвер. Помогите нематематику

[stanley]

коллеги, есть сугубо практическая задача. выглядит как простая учебная, но ответа я найти не смог.

проводим эксперимент почти как в схеме Бернулли. в результате эксперимента измеряется величина x (неотрицательна по определению). вероятность p того, что x>0, достаточно мала. однако в отличие от классической схемы Бернулли, сама x является случайной с известным распределением (возможно как дискретное, так и непрерывное).

задача. найти распределение суммы измеренных x в n независимых испытаниях.

[--mS--]

Существо вопроса не очень понятно. Чтобы находить распределение суммы независимых случайных величин, нужно знать их распределения, а не только величину атома в нуле.
В отсутствие этой информации можно предложить только общие (и практически бесполезные) рецепты типа формулы свёртки для функций распределения: $F_{X_1+X_2}(x) = \mathsf P(X_1+X_2 < x) =\int\limits_{-\infty}^\infty F_{X_1} (x-t)\,d F_{X_2}(t)$.
Разве что вот такие вероятности в условиях задачи одни и те же, независимо от распределения $X_i$: $\mathsf P(X_1+\ldots+ X_n =0)=(1-p)^n$, $\mathsf P(X_1+\ldots+ X_n >0)=1-(1-p)^n$. А дальше распределение определяется распределением $X_i$.

[stanley]

попробую конкретизировать.

самый простой вариант.

пусть
$X \sim N(\mu,\sigma)$

$Y = \left\{ \begin{array}{1} X p, \\ 0 (1-p) \end{array}\right$

$Z = \sum\limits_{i=1}^n Y_i$

для начала будем считать, что n - детерминированный параметр. хотя на практике это тоже случайная величина
задача - определить распределение Z

[--mS--]

$X \sim N(\mu,\sigma)$

Только мне привычно обозначение $N(\mu,\sigma^2)$, где $\sigma^2$ - дисперсия, я его ниже и использую.
Вижу такой простой путь: свяжем с каждой величиной $Y_i$ не только саму $X_i\sim N(\mu,\sigma^2)$, но и независимую от всего остального бернуллевскую $\alpha_i \sim B(p)$. Тогда $Y_i = \alpha_i X_i$.

Найдем функцию распределения суммы:

$$\mathsf P\left(\sum_{i=1}^n \alpha_i X_i < x\right) = \sum_{k=0}^n \mathsf P(A_k),$$

где событие $A_k$ состоит в том, что $n-k$ штук из "альф" обратились в ноль, а остальные $k$ равны единице, и при этом сумма игреков меньше $x$. По формуле Бернулли получаем для $k \geq 1$

$$\mathsf P(A_k) = C_n^k p^{n-k}(1-p)^{k} \cdot \mathsf P(X_1+\ldots+X_{k} < x)= C_n^k p^{n-k}(1-p)^{k} \cdot \textrm{Ф}_{\mu k,\, \sigma^2 k}(x).$$

Здесь использован тот факт, что сумма независимых нормальных величин снова нормальна, и матожидания-дисперсии складываются. Можно функцию распределения нормального закона выразить через стандартную нормальную

$$\textrm{Ф}_{\mu k, \,\sigma^2 k}(x) = \textrm{Ф}_{0,\,1}\left(\frac{x-\mu k}{\sigma \sqrt k}\right)$$

Осталось слагаемое при $k=0$, когда все альфы нулевые:

$$\mathsf P(A_0) = (1-p)^n \cdot \mathsf P(0 < x).$$

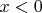
Это скачок в нуле: при $x < 0$ функция распределения суммы равна

$$\mathsf P\left(\sum_{i=1}^n \alpha_i X_i < x\right) = \sum_{k=1}^{n} C_n^k p^{n-k}(1-p)^{k} \cdot \textrm{Ф}_{0,\,1}\left(\frac{x- \mu k}{\sigma \sqrt k}\right),$$

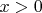
а при $x > 0$ добавляется ещё одно слагаемое $(1-p)^n$.

Интересующее нас распределение есть просто смешанное распределение: его функция распределения есть выпуклая линейная комбинация нормальных распределений (с весами = биномиальным вероятностям) и распределения, вырожденного в нуле.

[stanley]

огромное спасибо.

идея решения понятна, буду пробовать другие распределения X и пытаться учесть неопределенность n

[Dan B-Yallay]

stanley в сообщении #217199 писал(а):

в результате эксперимента измеряется величина x (неотрицательна по определению). вероятность p того, что x>0, достаточно мала. .

[stanley]

Dan B-Yallay в сообщении #219572 писал(а):

stanley в сообщении #217199 писал(а):

в результате эксперимента измеряется величина x (неотрицательна по определению). вероятность p того, что x>0, достаточно мала. .

а что тут противоречивого?