Найти область сходимости степенного ряда

[rar]

Поправил.

Найти область сходимости степенного ряда

$$\sum\limits_{n=0}^{\infty}(-1)^nx^{2n}$$

.


Перепишем так:

$$\sum\limits_{n=0}^{\infty}(-1)^n(x^{2})^n$$

(ряд, кстати, знакочередующийся)

Далее не понятно как с помощью формулы Даламбера

$$R=\lim_{n\to\infty}\left|\frac{a_n}{a_{n+1}}\right|$$

исследовать сходимость этого ряда.

За что

$$a_n$$

принимать? Получается, что

$$a_n=(-1)^n$$

, а

$$a_{n+1}=(-1)^{n+1}$$

.

Тогда выходит так:

$$R=\lim_{n\to\infty}\left|\frac{(-1)^n}{(-1)_{n+1}}\right|=\lim_{n\to\infty}1=1$$

. Тогда

$$-1<x^2<1$$

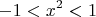
. И область сходимости равна

$$-1<x<1$$

.

Исследуем ряд на концах интервала.

$$\sum\limits_{n=0}^{\infty}(-1)^n[(\pm 1)^{2}]^n=\sum\limits_{n=0}^{\infty}(-1)^n$$

- поведение будет одинаково на обоих концах.

Проверим необходимое условие сходимости ряда

$$\lim_{n\to\infty}(-1)^n$$

. При стремлении

$$n\to\infty$$

получается то

$$1$$

, то

$$-1$$

. Соответственно предела не существует. По необходимому условию сходимости этот ряд расходится.
И область сходимости интервала есть

$$-1<x<1$$

.

Ответ: область сходимости степенного ряда

$$-1<x<1$$

.

[Brukvalub]

rar в сообщении #214829 писал(а):

Верно я делаю или нет?

Верно, но нужно еще исследовать сходимость на концах.

[rar]

Я там, кстати, справил. Непонятки теперь с исследованием на концах интервала.

[ewert]

rar в сообщении #214829 писал(а):

Вот тут недопонимание. Получается, что ряд ни сходящийся, ни расходящийся. Так что ли?

Что ли не так. Проверьте необходимое условие сходимости.

[Brukvalub]

rar, Вы когда-нибудь слышали что-нибудь о необходимом условии сходимости ряда?

[Ёж]

как я понимаю данный ряд содержит только четные степени $x$. Следовательно, все коэффициенты перед нечетными степенями $x$ равны нулю. Можно ли в данном случае применить формулу

$$R=\lim_{n\to\infty}\left|\frac{a_n}{a_{n+1}}\right|$$

?

Может лучше применить признак Даламбера

$$\lim_{n\to\infty}\left|\frac{f_{n+1}(x)}{f_{n}(x)}\right|$$

?

[rar]

Проблемы с пределом возникли. Помогите.

[ewert]

rar в сообщении #214829 писал(а):

Проверим необходимое условие сходимости ряда

$$\lim_{n\to\infty}(-1)^n$$

- вот проблемка, чему равен придел?

"Тоже мне бином Ньютона". Просто докажите, что для любой наперёд заданной церкви этот придел не существует.

[rar]

Ну при стремлении

$$n\to\infty$$

получается то

$$1$$

, то

$$-1$$

. Соответственно предела не существует.
И что отсюда следует? Каково поведение на концах интервала?

[Brukvalub]

rar в сообщении #215946 писал(а):

И что отсюда следует? Каково поведение на концах интервала?

Brukvalub в сообщении #215383 писал(а):

rar, Вы когда-нибудь слышали что-нибудь о необходимом условии сходимости ряда?

[rar]

Да. Если есть придел, то необходимое условие сходимости выполнено. В моем случае предела нет. Значит на концах интервала ряда расходится. И область сходимости интервала есть

$$-1<x<1$$

.

[Brukvalub]

rar в сообщении #215963 писал(а):

Да. Если есть придел, то необходимое условие сходимости выполнено.

Это неверно. Вам лень прочитать в любом учебнике по анализу формулировку необходимого условия сходимости ряда, и, при этом вы надеетесь, что вам здесь будут тупо раз за разом повторять одно и то же?
вы нас за попугаев держите?

[rar]

Прочитаю... Спасибо.

-- Пт май 22, 2009 15:16:00 --

Вроде, подправил в конце.

-- Пт май 22, 2009 22:22:19 --

Вроде поправил. Думаю теперь-то верно.

[Brukvalub]

rar в сообщении #214829 писал(а):

Соответственно предела не существует. И соответственно он отличен от нуля. По необходимому условию сходимости этот ряд расходится.

Второе предложение - лишнее.

[rar]

Спасибо. Поправил.