собственные числа

[terminator-II]

дана матрица $A=(a_{ij})$ состоящая из положительных элементов. доказать, что по крайней мере одно из собственных чисел этой матрицы $\ge\max_i \{a_{ii}\}$.

[ewert]

Выжимка из теоремы Перрона-Фробениуса: если все элементы матрицы положительны, то у неё есть положительное собственное число, равное её спектральному радиусую.

[terminator-II]

ewert в сообщении #214475 писал(а):

Выжимка из теоремы Перрона-Фробениуса: если все элементы матрицы положительны, то у неё есть положительное собственное число, равное её спектральному радиусую.

не понял связи

[ewert]

Допустим для простоты, что максимальный диагональный элемент сидит в верхнем левом углу. Возьмём вектор $\vec x_0=(1,0,0,\ldots)$ и затем $\vec x_{n+1}=A\vec x_n$, т.е. $\vec x_n=A^n\vec x_0$. Из неотрицательности элементов матрицы очевидно, что $\|\vec x_n\|\geqslant (a_{11})^n=(a_{11})^n\|\vec x_0\|$. 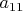А это означает, что $\|A^n\|$ не меньше $(a_{11})^n$ и, следовательно, спектральный радиус матрицы не меньше $a_{11}$.

[terminator-II]

ok про теорему Перрона-Фробениуса я до сего момента не слышал, хотя ,конечно, ясно, что ничего нового в этой науке быть не может. само утверждение я выводил из соображений дифуров

[ewert]

terminator-II в сообщении #214517 писал(а):

про теорему Перрона-Фробениуса я до сего момента не слышал,

Я, каюсь, тоже не слыхал, просто посмотрел в книжках, что вообще известно про матрицы с положительными элементами.

[RIP]

Можно ещё так. Рассмотрим непрерывное отображение симплекса $x_1+\ldots+x_n=1$, $x_i\ge0$, в себя:
$y_i=\bigl(\sum_{i,j=1}^na_{i,j}x_j\bigr)^{-1}\sum_{j=1}^na_{i,j}x_j$.
По теореме Брауэра, найдётся неподвижная точка. Это собственный вектор, все компоненты которого положительны, поэтому соответствующее собственное значение $\ge\max a_{i,i}$.