Построение позициоонной системы счисления

[ellipse]

Лемма: Если фиксировать число $q>1$, то для любого положительного $x\in R$ найдется единственное целое $k\in Z$ такое, что $q^{k-1}\leqslant x<q^k$

Далее выбирается такое число p, что $q^{p}\leqslant x<q^{p+1}$ (1)

По принципу Архимеда найдем единственное натурально число $a_{p}\in N$ такое что

$a_{p}q^{p}\leqslant x<a_{p}q^p+q^p$ (2)

Учитывая (1), можно утверждать что $a_{p}\in \{1,2, ..., q-1\}$

Из соотношения (2) и п.Архимеда следует, что существует единственное $a_{p-1}\in \{1,2, ...,q-1\}$ такое что

$a_{p}q^{p}+a_{p-1}q^{p-1}\leqslant x<a_{p}q^{p}+a_{p-1}q^{p-1}+q^{p-1}$

Как получилось последнее выражение?

[Алексей К.]

До прихода специалистов, знающих принцип Архимеда (мне что-то помнится только в связи с плавающими числами: на число, опущенное в жидкость, действует какая-то там выталкивающая сила), советую уточнить:

ellipse писал(а):

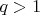
Лемма: Если фиксировать число $q>1$, то для любого положительного $x\in R$ найдется единственное целое $m\in Z$ такое, что $q^{k-1}\leqslant x<q^k$

что $q$ --- видимо целое (или нет?)
где $m$ фигурирует дальше? перепутано с $k$?

ellipse писал(а):

Далее выбирается такое число p, что $q^{p}\leqslant x<q^{p+1}$ (1)

А чо его выбирать, если по предыдущей формуле $p=k-1$ подходит?

[ellipse]

Цитата:

что $q$ --- видимо целое (или нет?)

Произвольное вещественное

Цитата:

где $m$ фигурирует дальше? перепутано с $k$?

Да, конечно, уже исправил

[EtCetera]

Понятия не имею, что такое "принцип Архимеда", но элементарные соображения подсказывают, что нужно действовать так:
Вычтем из (2) $a_{p}q^{p}$ и обозначим $x'=x-a_{p}q^{p}$. Получим
$0\le x'<q^p$
Для $x'$ также можно записать соотношение (2). Т.к. $x'<q^p$, то оно будет иметь вид
$a_{p-1}q^{p-1}\le x'<a_{p-1}q^{p-1}+q^{p-1}$ (2')
Прибавляя к (2') $a_{p}q^{p}$, получаем искомое двойное неравенство.
Примечание.
$a_{p-1}$ может быть, в отличие от $a_p$, равно 0.