Когда я задавал вопрос я имел в виду следующее.
Для начала нужно опеределить кратность корня. Начнём с полиномов.
1. Полином степени 
Пусть дан полином

степени

с вещественными или комплексными коэффициентами:

Из алгебры известно, что его можно разложить на множители

где

--- нуль полинома,

--- его кратность (по определению),

.
Пусть числа

,

и

лежат в области

. Тогда "сумма корней уравнения

, лежащих в области

" есть

.
2. Функция  , аналитическая в области
, аналитическая в области 
Пусть у функции

имеется конечное число решений уравнения

, расположенных в области

, пусто это будут

,

,

. Например, в окрестности точки

имеем

где

. Назовём число

--- нулём кратности

функции

. Это определение применимо и для

,

, и к тому же оно не противоречит кратности нуля для полиномов (это обобщение этого понятия).
Тогда задача "найти сумму решений уравнения

, лежащий в области

" имеем своим ответом сумму

.
Для аналитических функций, как и для полиномов в области

вполне корректно определено понятие кратности корня или решения уравнения и поэтому вопрос "сумма решения, лежащих в области

" поставлен корректно и имеет однозначную трактовку.
Если бы нужна была сумма

, то следовало бы поставить вопрос так: "сумма различных решений, лежащих в области

".
3. Функция  непрерывная, но не аналитическая в
непрерывная, но не аналитическая в 
Рассмотрим простой пример:

Очевидно, что функция непрерывная, однако она не имеет производной в точке

. В этой же точке
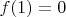
. Определить для такой функции порядок нуля (или кратность) невозможно (
по определению).
Для этой функции и подобных ей вопрос "сумма корней уравнения, лежащих в области

" следовало бы трактовать (а значит и задавать) в таком виде: "сумма различных решений уравнения, лежащих в области

".
Рассмотрим пример, с которого я начал тему:

Перепишем это так

и

.
Легко убедиться, что

Задание с формулировкой "найти сумму корней уравнения ..." следовало бы трактовать по-разному, в зависимости от функции (
1,
2 или
3).
В такой формулировке для рассмотренного примера задача не имеет смысла, однако имеет смысл вопрос "сумма различных решений уравнения,

".
Если бы подобный вопрос был задан на устном экзамене (а об экзамене речь и идёт), то всё в порядке: можно разъяснить что да как, но если экзамен письменный --- формулировки должна быть чёткими, не предполагающими разных трактовок.
"Задав глупый вопрос, не ожидай на него внятный ответ".
Это я о себе :-)).
Вопрос (который я так и не задал в первом сообщении): можно ли определить кратность корня по-другому, чтобы задача в первоначальной формулировке имела смысл?
ewert писал(а):
Очень даже аналитическая. На своей области аналитичности. Вы, похоже, путаете функции аналитические и целые.
Целые и аналитические функции различаю, с этим, слава богу, всё в порядке, однако "язык мой --- враг мой" :-))
Я имел в виду функцию

(см. выше).
VAL писал(а):
В школьном курсе, вообще, и в заданиях ЕГЭ, в частности, никаких кратных корней нет.
Комметрировать не буду. Но математическая культура, как и и всякая культура, закладывается с детства, и учить ТАК ребят в школе я считаю кощунством. Но обсуждать решения министерства образования, как головой в чан с дерьмом, прощу прощения у более культурной части форума.
VAL писал(а):
Если же говорить более серьезно, приведенная цитата показывает, что приоритет отдается подсчету корней без учета кратности. Но без догматизма.
Мне эта фраза говорит лишь о том, кто составлял и для кого учебник. Никогда не был доволен изложеним материала в школьных учебниках.
ewert писал(а):
Кстати, я считаю это методически правильным. Рассказывать про комплексные числа в школе (средней) хоть сколько-то всерьёз -- немыслимо.
Про вещетсвенные числа --- тоже? Повторю свою мысль: рассказывать нужно, но вопрос в объёме (сколько по вашему "всерьёз"?), и как это сделать методически. Мне кажется, если и делать такую работу, то нужно перестраивать весь школьный курс математики. Но это моё личное мнение.