Условие:
Дифракционная картина наблюдается на расстоянии  от точечного источника монохроматического света с длиной волны
от точечного источника монохроматического света с длиной волны  . Посередине между экраном и источником помещена диафрагма с круглым отверстием. При каком радиусе отверстия центр дифракционной картины, наблюдаемый на экране, будет наиболее темным?
. Посередине между экраном и источником помещена диафрагма с круглым отверстием. При каком радиусе отверстия центр дифракционной картины, наблюдаемый на экране, будет наиболее темным?
Видимо надо пользоваться этой формулой

. В моем случае радиус отверстия получается

.

- число зон Френеля укладывающихся в отверстии. А вот какое оно должно быть? Знаю, что при четном

в центре дифракционной картины будет темное пятно. А вот какое четное

должно быть? И как его определить? Объясните пожалуйста. Спасибо.
Добавлено спустя 1 час 33 минуты 30 секунд:
Я так понял, нужно брать самое маленько четное

, т.е.
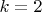
. Как думаете?
Добавлено спустя 18 минут 42 секунды:
Так, давайте я напишу, то что у меня получается. А вы проверите.
Радиус отверстия будет равен

. В центре дифракционной картины будет наблюдаться наиболее темное пятно при наименьшем четном числе зон Френеля:
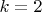
.
Делаем подстановку чисел и вычисляем:

.
Ответ:

.