Собственно, интересуюсь, что такое сабж, и с чем его едят. Метка "срочно" - потому, что в понедельник я и сам в библиотеку схожу и всё узнаю, наверное.

Ну то есть наблюдаю такое рассуждение: берется непрерывная неубывающая на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
функция

, у нее модуль непрерывности
![$\omega(\delta)=\sup\limits_{|x-y|<\delta\atop x,y\in[a,b]}|\sigma(x)-\sigma(y)|$ $\omega(\delta)=\sup\limits_{|x-y|<\delta\atop x,y\in[a,b]}|\sigma(x)-\sigma(y)|$](https://dxdy-04.korotkov.co.uk/f/7/9/6/7960adf4903340a74176b2ed8a162e0f82.png)
,
и утверждается, что по некой лемме Стечкина тогда существует
выпуклая вверх функция
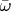
такая, что

при

. Что за лемма тут имеется ввиду, и где можно про нее почитать?
upd: упс, неправильно лемму написал. Правильно
