задачи на прогрессии

[oskolok]

Здравствуйте!
Помогите, пожалуйста, решить...
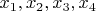
1. Пусть $x_1$ и $x_2$ - корни уравнения $3x - x^2 = A$, a $x_3$ и $x_4$ - корни уравнения $12x - x^2 = B$. Известно, что последовательность $x_1, x_2, x_3, x_4$ является геометрической прогрессией, все члены которой положительные. Найти значения А и В.
2. Найдите четырехзначное натуральное число, в котором цифра тысяч, цифра сотен и двузначное число, составленное из двух его последних цифр, образуют геометрическую прогрессию, а его три последние цифры - арифметическую прогрессию.

Заранее огромное спасибо ^_^

[TOTAL]

oskolok писал(а):

1. Пусть $x_1$ и $x_2$ - корни уравнения $3x - x^2 = A$, a $x_3$ и $x_4$ - корни уравнения $12x - x^2 = B$. Известно, что последовательность $x_1, x_2, x_3, x_4$ является геометрической прогрессией, все члены которой положительные. Найти значения А и В.

Сначала найдите $x_1, x_2, x_3, x_4.$ Затем найдите А и В

[BVR]

По второй задаче. Если число $abcd$ и $q$ знаменатель прогрессии. То имеем $b=aq$ и $aq^2=10c+d$. Учитывая, что $c$ есть среднее арифметическое $b$ и $d$, можно доказать, что $q>=5$. А, значит, $a$ может быть только 1. Ну и там легко получить число.

Добавлено спустя 5 минут 59 секунд:

Это год, в котором родился Владимир Андреевич Стеклов, российский математик.

Добавлено спустя 3 минуты 19 секунд:

И умер Джодж Буль.

[Лиля]

Запишите уровнения в виде:
$-(x-p^{0}x_1)(x-p^{1}x_1)=0$ и
$-(x-p^{2}x_1)(x-p^{3}x_1)=0$
расскройте скобки найдите коэфициенты $a_1,b_1,c_1,a_2,b_2,c_2$ из выше стоящих уровнений и прировнияйте к соответствующим коэфициентам ваших уровнений -посмотрите вийдит ли что

[oskolok]

спасибо большое!
все получилось^^