Задача Эрдёша

[Imperator]

Пусть $p$ -- простое число, большее 3, и $n=\frac{2^{2p}-1}{3}.$ Докажите, что $2^n-2$ делится на $n.$

[Руст]

Насколько помнится это я уже решал в Mathlinks. Jcnfdkz. lheubv/

[Sonic86]

Можно так решить:
Сначала избавимся от тройки в знаменателе.
Заметим, что $2^n-2$ делится на 3, а $\gcd (2^{n-1}-1, (2^{n-1})^2+2^{n-1}+1) = \gcd (2^{n-1}-1, 3)=3$, поэтому $2(2^{n-1}-1) \equiv 0 (n)$ равносильно $2(2^{n-1}-1)(2^{n-1})^2+2^{n-1}+1) \equiv 2(2^{3(n-1)}-1) \equiv 0 (3n)$, то есть $2(2^{4^p-4}-1) \equiv 0 (2^{2p}-1)$ (1). А так как если $m$ делится $n$, то $2^m-1$ делится на $2^n-1$, то (1) следует из $4^p-4 \equiv 0 (2p)$, что верно по малой т.Ферма.

[Imperator]

Можно и так решить.


Пусть $p>3$. По малой теореме Ферма $2^{p-1}-1$ делится на $p$. Но в то же время 3 является делителем $2^{p-1}-1.$ Значит, $2^{p-1}-1$ делится на $3p.$

По условию $n=\frac{2^{2p}-1}{3}.$ Следовательно, $2^{2p}-1$ делится на $n.$

Рассмотрим $n=\frac{2^{2p}-1}{3}\equiv\frac{2^{2p}-4+3}{3}\equiv \frac{2^{2p}-4}{3}+1\equiv\frac{4(2^{p-1}-1)(2^{p-1}+1)}{3}+1$ $\Longrightarrow$
$n-1=\frac{4(2^{p-1}-1)(2^{p-1}+1)}{3}.$
$2^{p-1}-1=3pq (q\in\mathbb{N})$ $\Longrightarrow$
$n-1=4pq(2^{p-1}+1)$ $\Longrightarrow$ $n-1$ делится на $2p.$
Так как $n-1$ делится на $2p,$ то $2^{n-1}-1$ делится на $2^{2p}-1.$ В свою очередь, $2^{2p}-1$ делится на $n,$ значит, $2^{n-1}-1$ тоже делится на $n.$ Тогда понятно, что и $2\cdot(2^{n-1}-1)\equiv 2^n-2$ делится на $n.$

[Imperator]

Еще одна задача Эрдёша.


Дано целое число $k\leqslant\frac{n^2}{4},$ не имеющее простых делителей, больших $n$. Докажите, что
$n!\equiv0$ $(mod$ $k).$

[Руст]

Тривиальный вопрос сводится к случаю $k=p^l$ и к неравенству $frac{p^k-1}{p-1}>2k+1,k>1$.

[Imperator]

Руст писал(а):

Тривиальный вопрос сводится к случаю $k=p^l$ и к неравенству $frac{p^k-1}{p-1}>2k+1,k>1$.

Для меня нетривиально. Можно чуть подробнее?

[Руст]

Пусть $p^m\le n<p^{m+1}$, тогда $ord_p(n!)\ge \frac{p^m-1}{p-1}$ и $ord_p(k)\le 2m+\epsilon$ где $\epsilon =1,p>4$ иначе 0. Случай m=1 можно рассмотреть отдельно.

[Imperator]

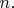
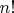
Пусть $p$ -- произвольный простой делитель числа $k,$ не имеющего простых делителей, больших $n.$ Тогда $p\leqslant n,$ следовательно, $n!$ делится на $p.$

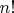
Пусть в каноническое разложение $k$ число $p$ входит в четной степени $2l$ ($l\in \mathbb{N}$). Из $k\leqslant\frac{n^2}{4}$ получаем, что $2p^l\leqslant n.$ Значит, показатель, с которым $p$ входит в $n!,$ не меньше $2p^{l-1}\geqslant 2l,$ значит, $n!$ делится на $p^{2l}.$

Пусть теперь в каноническое разложение $k$ число $p$ входит в четной степени $2l+1$ ($l\in \mathbb{N}$). Из $k\leqslant\frac{n^2}{4}$ получаем, что $2\sqrt{p}p^l\leqslant n$ (*). Рассмотрим 2 случая:
1. $4p^{l}<n.$ Очевидно, что в этом случае $p^{2l+1}|n!.$
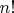
2. $4p^{l}\geqslant n$ (**). Сравнивая (*) и (**), получим, что $\sqrt{p}\leqslant 2$ $\Longrightarrow$ $p\leqslant 2\sqrt{p}$ $\Longrightarrow$ $p^{l+1}\leqslant n.$ Поэтому показатель, с которым $p$ входит $n!$, не меньше
$p^l+p^{l-1}+...+p+1\geqslant 2^l+2^{l-1}+...+2+1=2^{l+1}-1\geqslant 2l+1.$ Следовательно, в этом случае тоже $p^{2l+1}|n!.$

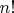
Итак, действительно, $n!$ делится на $k.$

Добавлено спустя 16 минут 20 секунд:

Еще одна задача Эрдёша.

Даны $n+1$ натуральных чисел $a_1,a_2,...,a_{n+1},$ каждое из которых не больше $2n.$ Доказать, что по крайней мере одно из них делится на какое-то другое число из того же набора.

[Руст]

Каждое число можно представить в виде $a=b*2^k$, где b нечётное. Так как в последовательности, где нет делителей между членами не может встречаться два члена с одним и тем же b, т.е. их не больше n.

[Imperator]

Руст, вы опять правы. Браво!

[Руст]

Здесь получилось, что найдётся два числа, что отношение является степенью двойки.
Предлагаю в качестве задачи какое максимальное количество чисел можно выбрать из множества ${1,2,...,n\}$ так, чтобы среди них не встречались два разных числа, отношение которых некоторое произвольное (не заданное заранее) целое нечётное число.

[Imperator]

Есть предположение, что нужно взять все простые $\leqslant n$ "+" все натуральные степени 2, лежащие на промежутке $[1,n].$ Их общее количество и даст требуемый максимум.

Добавлено спустя 5 минут 59 секунд:

Еще одно предположение: $\left[ \frac n 2 \right]+1.$

[Руст]

Похоже вы не решили эту задачу сами. Важно только в множестве S допустимых отношений выбрать минимальное k. Таким же образом все числа вида $x=yk^l,k\not|y$ разделит на классы. Множество $\{[n/k]+1,[n/k]+2,....n\}$ ровно один элемент из любого класса, т.е. представляет максимальное множество с требуемым свойством с количеством элементов $m=n-[n/k]$. Любое множество с количеством элементов больше m, содержит два элемента, отношение которых есть некоторая степень k. В нашем случае k=3.

[Imperator]

Еще 2 задачи Эрдёша.

1. Неравенство для НОК.
Пусть $a_1<a_2<...<a_n\leqslant 2n$ -- конечная последовательность положительных целых чисел.
Доказать, что
$min[a_i,a_j]\leqslant 6([\frac{n}{2}]+1),$
где $[a_i,a_j]$ -- НОК $a_i$ и $a_j.$
Эту оценку для $min[a_i,a_j]$ нельзя улучшить.

2. Неравенство для НОД.
Пусть $a_1<a_2<...<a_n < 2n$ -- конечная последовательность положительных целых чисел.
Доказать, что
$max(a_i,a_j)>\frac{38n}{147}-c,$
где $(a_i,a_j)$ -- НОД $a_i$ и $a_j,$ а $c$ не зависит от $n.$
Эту оценку для $max(a_i,a_j)$ нельзя улучшить.