t_dream писал(а):
В книге Прудникова, Бычкова и Марычева есть следующий интегральное равенство, хотелось бы узнать с помощью какой замены переменных оно получено
![\int\limits^\infty_{-\infty}\dots \int\limits^\infty_{-\infty}\frac{dx}{(p^2+(\vec x-\vec a)^2)^\mu(q^2+(\vec x-\vec b)^2)^\nu}=\frac{\pi^{n/2}\Gamma(\mu+\nu-n/2)}{\Gamma(\mu)\Gamma(\nu)}\int\limits^1_0\frac{t^{\mu-1}(1-t)^{\nu-1}dt}{[p^2t+q^2(1-t)+t(1-t)(\vec a-\vec b)^2]^{\mu+\nu-n/2}},\quad{\rm Re}\,\mu>0,{\rm Re\m}\nu>0 \int\limits^\infty_{-\infty}\dots \int\limits^\infty_{-\infty}\frac{dx}{(p^2+(\vec x-\vec a)^2)^\mu(q^2+(\vec x-\vec b)^2)^\nu}=\frac{\pi^{n/2}\Gamma(\mu+\nu-n/2)}{\Gamma(\mu)\Gamma(\nu)}\int\limits^1_0\frac{t^{\mu-1}(1-t)^{\nu-1}dt}{[p^2t+q^2(1-t)+t(1-t)(\vec a-\vec b)^2]^{\mu+\nu-n/2}},\quad{\rm Re}\,\mu>0,{\rm Re\m}\nu>0](https://dxdy-01.korotkov.co.uk/f/8/3/0/830a627ad120c0ff5d090896db9c5b8382.png)
n - размерность векторного пространства, в котором проходит интегрирование, например

Те, кто знакомы с расчетом феймановских интегралов сразу увидят феймановскую параметризацию:

или при вещественных положительных

и комплексных

с

,
или при ненулевых комплексных

и натуральных

.
Второй вариант используется для расчета диаграмм в методе размерной регуляризации.
Отсюда сразу при

получаем:
(
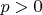
,

,

,

,

)



сдвиг

и интеграл
(

,

)

замена

,


замена

,



дает при

и



что и требовалось доказать.
Замечание: параметризационная формула для натуральных

доказывается из ее простой версии (для

):

- либо путем дифференцирования по

, что дает


,
либо группировкой и интегрированием переменных

при одинаковых

по принципу

и


, что приводит к

Сама же простая версия доказывается либо по индукции, либо общим методом. Доказательства приведу позже (они есть в учебниках).
Теперь главное:
Доказательство для нецелых  НЕИЗВЕСТНО!!!
НЕИЗВЕСТНО!!!
хотя эта формулировка безответственно встречается в учебниках (будьте бдительны!)
Мое мнение: для нецелых

это параметрическое тождество попросту
НЕВЕРНО!