arqady писал(а):
VAL писал(а):
А в этой задаче условие непонятное.
Что такое "строгий треугольник"?
Что такое
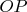
?
Ну до этого даже я могу догадаться:
А почему "даже"?
Цитата:
имеется в виду остроугольный треугольник, точка

внутри него и

- центр описанной около этого треугольника окружности.
У меня были такие же подозрения насчет

.
А вот гипотеза про "строгость" была другая. Я полагал, этот термин означает, что вершины не лежат на одной прямой. Иными словами, "строгий треугольник" - это просто треугольник, а "нестрогий треугольник" - это просто тройка точек и отрезков, с концами в этих точках.
Впрочем, версию остроугольности я тоже держал в уме, но не считал основной

PS: Сейчас заглянул в первое сообщение темы и поменял приоритеты
