дельта-функция в сферических координатах

[nckg]

ОК, тогда будем говорить более предметно.

Рассмотрим пространство функций, определённых в $\mathbb R^3$ и обладающих следующими свойствами:

1. $\psi(r,\theta,\varphi)\in C^\infty(\mathbb R^3)$
2. $\psi(0,\theta,\varphi)=\psi(0,0,0)$
3. $\psi(-r,\theta,\varphi)=\psi(r,\pi-\theta,\varphi+\pi)$
4. $\psi(r,\theta+2\pi,\varphi)=\psi(r,\theta,\varphi+2\pi)=\psi(r,\theta,\varphi)$
5. $\psi(r,\theta,\varphi)$ финитна по $r$, т.е. существуют $r_{\min}, ~r_{\max}$:
   $\psi(r,\theta,\varphi)=0$ при $r\notin[r_{\min}, r_{\max}]$.

(вроде ничего не забыл:))

Полученное пространство функций назовём пространством основных функций $\Sigma(\mathbb R^3)$. Сходимость в $\Sigma(\mathbb R^3)$ определим так:
$\psi_n\to \psi$ если все частные производные по $r,\theta,\varphi$ от $\psi_n$
сходятся к соответствующим частным производным от $\psi$ равномерно в $\mathbb R^3$.
Рассмотрим множество линейных непрерывных функционалов на нём, обозначим его как $\Sigma'(\mathbb R^3)$.

На первый взгляд, топологические пространства $\Sigma(\mathbb R^3)$ и $D(\mathbb R^3)$
гомеоморфны, и поэтому должно существовать взаимно однозначное соответствие между
$\Sigma'(\mathbb R^3)$ и $D'(\mathbb R^3)$ (даже гомеоморфизм).

Например, любой обобщённой функции в сферических координатах $\widetilde f\in\Sigma'(\mathbb R^3)$, которая является локально интегрируемой, можно поставить
в соответствие функцию из $D'(\mathbb R^3)$ следующим образом:
Пусть $\Psi(x,y,z)\in D(\mathbb R^3)$, тогда $\psi(r,\theta,\varphi)=\Psi(r\sin\theta \cos\varphi,r\sin\theta\sin\varphi,r\cos\varphi)\in \Sigma(\mathbb R^3)$
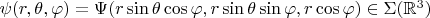
$(f,\Psi)=$(по определению)$=(\widetilde f, \psi)=$(тоже по определению)$=\int_0^{+\infty}dr\int_0^\pi d\theta \int_0^{2\pi}d\varphi ~ \widetilde f \cdot r^2\sin\theta \cdot \psi$,
поскольку $r^2\sin\theta \cdot \psi \in \Sigma(\mathbb R^3)$.

Это будет соответствовать привычным представлениям о замене координат.