Приводим к жордановой форме. Следим за любой Жордановой клеткой:

, где

получается из единичной матрицы

сдвигом главной диагонали на одну позицию вправо (т.е. вверх). Представляем логарифм от этой клетки в виде
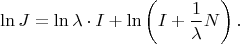
И формально раскладываем второе слагаемое в стандартный ряд Тейлора для логарифма. "В ряд" -- именно формально, фактически эта сумма будет конечной из-за нильпотентности матрицы

.
Полученный результат действительно будет логарифмом в том смысле, что будет выполняться тождество

-- потому, что все алгебраические манипуляции с матрицами в данном случае имеют те же формальные свойства (в т.ч. и коммутирование), что и обычные числа.
Неоднозначность полученного таким способом логарифма обусловлена неоднозначностью выбора ветви для

в каждой жордановой клетке.
Для прямого возведения в степень (

) схема ровно та же. Здесь неоднозначность вызвана неоднозначностью функции

для

(собственно, при иррациональных

эта неоднозначность именно к неоднозначности соответствующего логарифма и сводится).